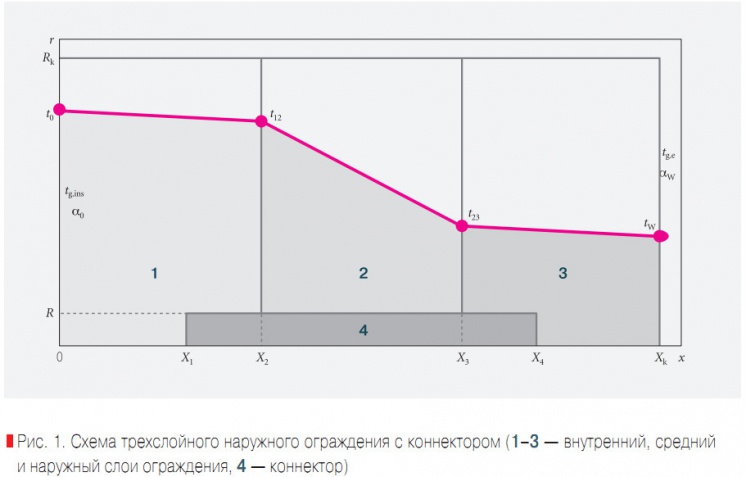
Рис. 1. Схема трехслойного наружного ограждения с коннектором
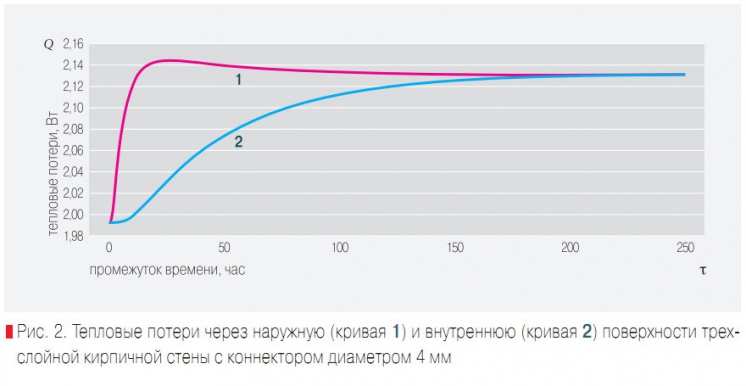
Рис. 2. Тепловые потери через наружную (кривая 1) и внутреннюю (кривая 2) поверхности трехслойной кирпичной стены с коннектором диаметром 4 мм
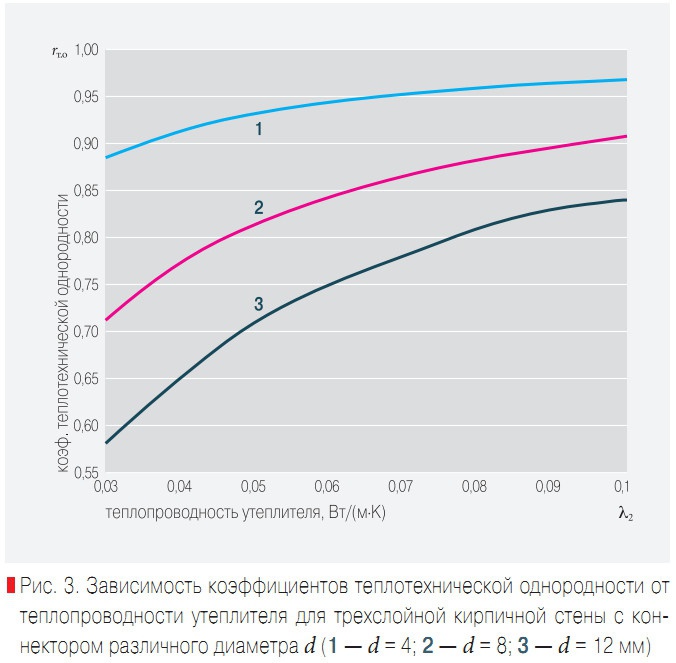
Рис. 3. Зависимость коэффициентов теплотехнической однородности от теплопроводности утеплителя для трехслойной кирпичной стены с коннектором различного диаметра d
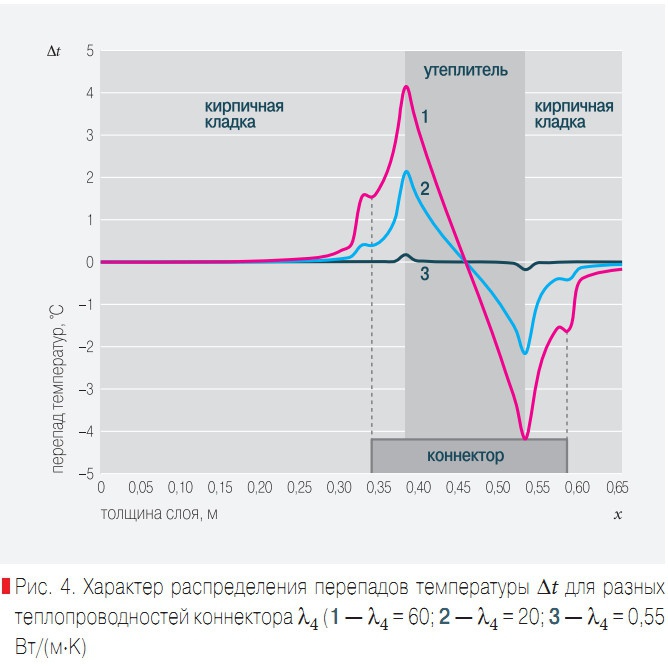
Рис. 4. Характер распределения перепадов температуры ∆t для разных теплопроводностей коннектор
В конструкциях наружных стен современных зданий сегодня все чаще используют различные соединительные гибкие и жесткие связи, шпонки, профили и кронштейны различных конструкций, которые необходимо учитывать при теплотехнических расчетах. Последние нормативные документы, такие как СНиП II-3–79* «Строительная теплотехника», СНиП 23-02–2003 «Тепловая защита зданий» и СП 23-101–2004 «Проектирование тепловой защиты зданий», не охватывают в полной мере всего множества конструктивных решений систем утепления.
В работе [1] очень подробно представлены данные по значениям коэффициентов теплотехнической однородности наружных стен, выполненных из кирпича, железобетона или ячеистого бетона с использованием металлических гибких связей. В работе [2] представлена методика расчета коэффициентов теплотехнической однородности наружных стен с вентилируемым воздушным зазором и выполнен анализ влияния различных параметров фасадной системы утепления на характеристики теплозащиты.
Таким образом, для оптимального проектирования энергосберегающих ограждающих конструкций зданий и разработки эффективных систем их наружного утепления очевидна необходимость теоретического исследования закономерностей теплопереноса в таких конструкциях. Рассмотрим теплоперенос через многослойное наружное ограждение на примере типичной трехслойной стены с включением в виде цилиндрического коннектора (рис. 1).
Внутренним и наружным слоями ограждения являются кирпичные кладки, средним слоем — утеплитель. Концы коннектора заделаны во внутренний и наружный слои ограждения. Индексы 1–3 характеризуют внутренний, средний и наружный слои ограждения, индекс 4 — коннектор. Заданы температуры наружной tg.e и внутренней tg.ins сред, а также коэффициенты теплоотдачи на наружной αw и внутренней α0 поверхностях ограждения.
Вне зоны влияния коннектора известен профиль температуры по толщине ограждения, полученный из аналитического решения одномерной стационарной задачи теплопроводности [3]. Сформулированную задачу будем решать в цилиндрической системе координат, начало которой расположим на внутренней поверхности стены, ось x направим по нормали к стене, ось r — вдоль нее; ось коннектора совместим с осью x (рис. 1).
При численном решении математическую область определения задачи {0≤x ≤δ, 0≤r ≤∞, 0≤t ≤tfin}заменим замкнутой расчетной областью (1) Теплоперенос в каждой из подобластей описывается нелинейным нестационарным двумерным уравнением теплопроводности:
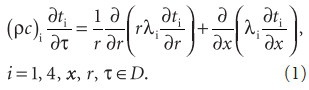
Система уравнений (1) замыкается начальными и граничными условиями:
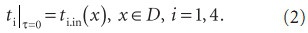
На границах расчетной области x = 0 и x = Xk выполняются условия конвективного теплообмена; на оси при r = 0 условия симметрии; на периферии области при r = Rk — условие независимости процесса теплопереноса от радиуса; на внутренних границах подобластей 1–4 — условия четвертого рода; D{0≤x≤Xk, 0≤r≤Rk, 0≤t≤tfin}—открытая расчетная область задачи. Численное решение задачи осуществлялось с помощью метода расщепления Н.Н. Яненко [4].
Полученные в результате расщепления одномерные уравнения теплопроводности в однослойных и многослойных областях в направлениях x и r рассчитывались итерационноинтерполяционным методом (ИИМ) [5]. Системы нелинейных разностных уравнений с трехдиагональными матрицами решались методом прогонки с итерациями по коэффициентам с заданной точностью.
Численное решение задачи по вышеизложенному алгоритму осуществлялось с помощью программы [6], разработанной на языке программирования ФОРТРАН. При создании программы использовался модульный принцип. Основной программный модуль, реализующий решение уравнения параболического типа общего вида с граничными условиями 1–4-го рода в однослойных и многослойных областях и состоящий из более мелких модулей расчета коэффициентов разностной схемы ИИМ и решения системы разностных уравнений с трехдиагональной матрицей методом прогонки, тестировался на известных аналитических решениях и решениях, полученных с помощью метода пробных функций.
Программа в целом без учета коннектора тестировалась на известном стационарном аналитическом решении [3].Модульный принцип построения программы позволяет быстро адаптировать ее под любую конфигурацию многослойного наружного ограждения с числом слоев, больше трех, и любую глубину заделки коннектора. Интерполяция исходных данных и результатов расчетов осуществлялась с помощью кубических сплайн-функций.
Для тестирования численного алгоритма и программы вначале была решена двумерная задача теплообмена в трехслойном ограждении без коннектора при постоянной температуре внешней среды. В результате численных расчетов было установлено, что независимо от задания начального условия, которое варьировало от –40 до +20°С, численное решение двумерной задачи стремится к единственному стационарному решению, совпадающему с известным аналитическим решением [3], что является одним из подтверждений достоверности результатов расчетов. При проведении базового расчета использовались значения параметров:
- λ1= λ3 = 0,8 Вт/(м •K); λ2=0,05 Вт/(м•K); λ4 = 60 Вт/(м•K);
- p1 = p3 = 1800 кг/м3; p2 = 150 кг/м3; p 4 = 7850 кг/м3;
- c1 = c3 = 880 Дж/(кг•К);
- c2 = 1340 Дж/(кг•К);
- c4 = 482 Дж/(кг•К);
- X1 = 0,33 м; X2 = 0,38 м; X3 = 0,53 м; X4 = 0,58 м;
- Xk = 0,65 м; Rk = 0,2 м;
- R = 0,002 м;
- α0 = 8,7 Вт/(м2•К);
- αw = 23 Вт/(м2•К);
- tg.ins = 20°С; tg.e = –40°С; tfin = 250 ч.
- Материал коннектора — арматурная сталь.
Расчет коэффициента теплотехнической однородности согласно (2), будем проводить по формуле
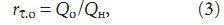
где Qо — тепловые потери через однородную стену, Qн — тепловые потери через неоднородную стену. Анализ рис. 2 показал, что при резком понижении температуры наружного воздуха с +20°С до –40°С через 24 ч после начала охлаждения тепловые потери с наружной поверхности стены достигают максимального значения, равного 2,15 Вт.
После выхода конструкции на стационарный режим теплопередачи тепловые потери через внутреннюю и наружную поверхности стены уравниваются и составляют примерно 2,13 Вт. Это служит одним из подтверждений достоверности расчетов. Характер поведения коэффициентов теплотехнической однородности в зависимости от теплопроводности утеплителя на рис. 3 показывает, что с увеличением теплопроводности утеплителя коэффициенты теплотехнической однородности возрастают.
Это объясняется тем, что при низких значениях теплопроводности утеплителя перенос теплоты осуществляется, в основном, по связи и в меньшей степени — по слою утеплителя. Значения коэффициента теплотехнической однородности для стены с утеплителем теплопроводностью 0,03 Вт/(м•К) составляют: для коннектора диаметром 4 мм— 0,89; 8 мм— 0,71 и 12 мм — 0,57; а с утеплителем теплопроводностью 0,08 Вт/(м•К) эти значения равны 0,97; 0,91 и 0,84 соответственно.
В работе [7] представлена методика расчета коэффициентов теплотехнической однородности наружных стен зданий с использованием аддитивных зависимостей. Эта методика предполагает использование коэффициентов эффективной теплопроводности характерных неоднородных слоев стены .В качестве характерного неоднородного слоя принимается слой стены с расположенными в нем теплопроводными включениями с неизменными поперечными сечениями.
Как показано в работе [8] внутри конструкции происходит распределение теплоты не только в поперечном, но и в радиальном направлениях (рис. 4). Поскольку зависимости из [7] этого распределения не учитывают, то они дают несколько меньшие значения коэффициентов теплотехнической однородности в сравнении с численными расчетами по математической модели.
Так, разница в значениях коэффициента теплотехнической однородности, полученных по методике из [7] и по математической модели составляет не более 6% для коннектора диаметром 4 мм; не более 7% — для коннектора диаметром 8 мм и не более 10%— для коннектора диаметром 12 мм (материал коннектора— арматурная сталь).
На рис. 4 показано влияние ТФХ материала коннектора на распределение перепадов температур: ∆t = t(x, r)|r = ∞ -- t(x,r)|r = 0 в различных сечениях x. Кривая 1 соответствует коннектору, выполненному из арматурной стали (λ4 = 60 Вт/(м•K), p 4 = 7850 кг/м3, c4 = 482 Дж/(кг•К), кривая 2 — коннектору из нержавеющей стали (λ4= 20 Вт/( м•K), p4= 5000 кг/м3, c4 = 800 Дж/(кг•К), кривая 3— коннектору из углепластика (λ4= 0,55 Вт/(м•K), p4= 1350 кг/м3, c4 = 1062 Дж/(кг•К).
Основная часть теплоты до сечения x = 0,455 м поступает в коннектор через боковые поверхности. Затем в зоне отрицательных температур теплота отводится от коннектора через его боковые поверхности и торец к материалам наружной стены. Наибольшие возмущения температурного поля происходят в зонах контакта внутреннего (x = 0,38 м) и внешнего (x = 0,53 м) слоев стены с утеплителем.Максимальное возмущение вносит коннектор, выполненный из арматурной стали, а минимальное — коннектор из углепластика.
Для них максимальные перепады температур ∆t равны 4,58 и 0,21°С соответственно. Для коннектора из нержавеющей стали ∆t = = 2,36°С.Можно отметить различие и в качественном поведении кривых. Для коннектора из углепластика, например, исчезают точки излома в местах стыка торцов коннектора с кирпичными кладками, что объясняется близостью коэффициентов теплопроводности кирпича и углепластика.
Таким образом, для точного определения теплового состояния и коэффициентов теплотехнической однородности трехслойных наружных стен зданий можно использовать разработанную программу [6], а для оценочных расчетов можно рекомендовать расчетные зависимости из [7]. Работа выполнена по программе Федерального агентства по образованию «Развитие научного потенциала высшей школы» (подпрограмма 2. Прикладные исследования и разработки по приоритетным направлениям науки и техники), код проекта 7756.
























