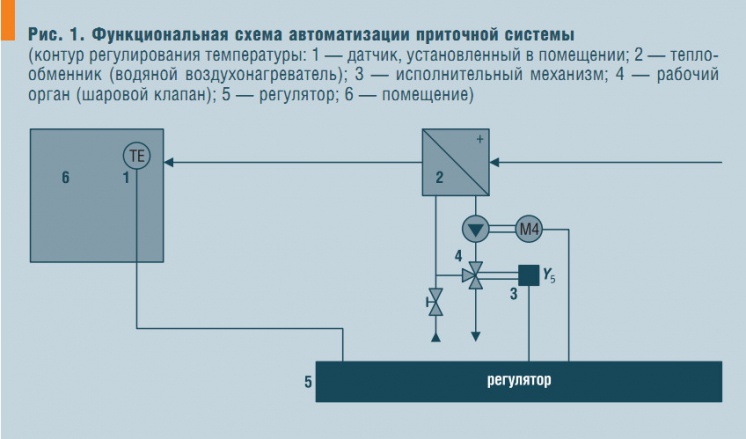
Рис. 1. Функциональная схема автоматизации приточной системы
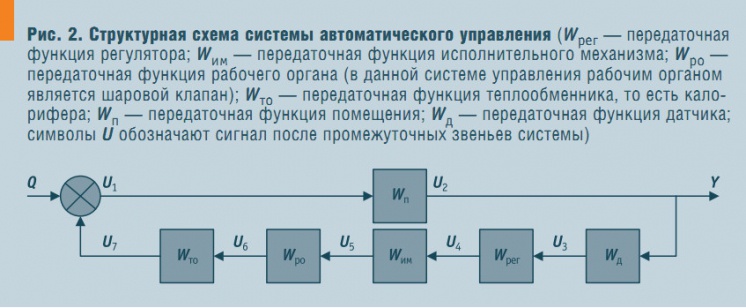
Рис. 2. Структурная схема системы автоматического управления
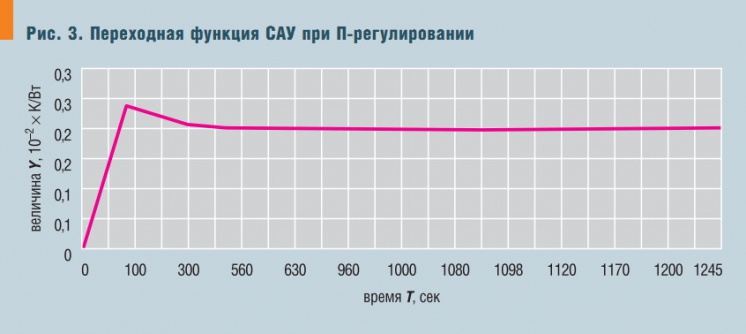
Рис. 3. Переходная функция САУ при П-регулировании
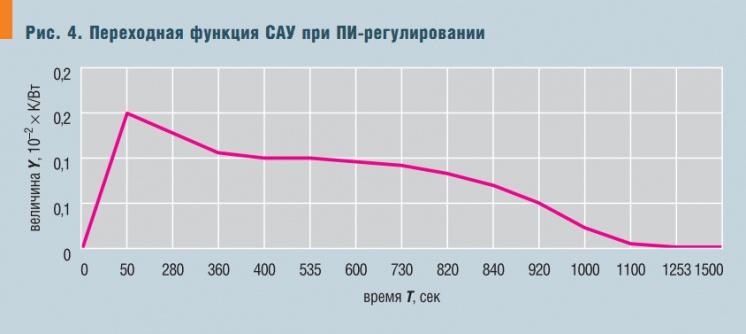
Рис. 4. Переходная функция САУ при ПИ-регулировании
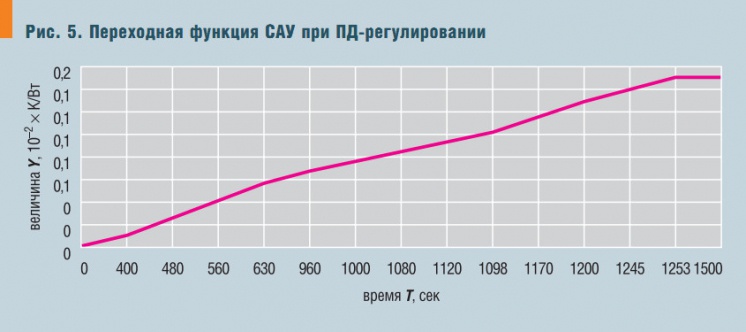
Рис. 5. Переходная функция САУ при ПД-регулировании
Внастоящий момент многие фирмы предоставляют оборудование для САУ, но до сих пор не предложена методика подбора коэффициентов регулятора на стадии проектирования САУ, учитывающая совместное функционирование и характеристики помещения и систем В и КВ [1]. Обычно предлагаемые в этом случае рецепты, например, в [2] и других подобных источниках, ссылающиеся в конечном счете на известную работу [3], дают очень упрощенные рекомендации, не использующие особенности работы элементов во всем контуре регулирования таких систем и замкнутый характер САУ.
В основном подбор коэффициентов для регуляторов производится уже на месте при наладке системы, фактически методом подбора этих коэффициентов. Рассмотрим простейшую модель САУ для приточной системы вентиляции. Пусть регулирование температуры в помещении происходит с помощью изменения температуры притока за счет регулировочного трехходового клапана, установленного в водяном контуре воздухонагревателя (калорифера).
Такой способ регулирования называется качественно-качественным, поскольку связан с изменением температуры теплоносителя при постоянном расходе. По датчику температуры, размещенному в рабочей зоне помещения, и по уставке, заданной оператором, контроллер в зависимости от используемого закона регулирования подает управляющий сигнал на электропривод регулировочного клапана.
Функциональная схема рассматриваемого контура регулирования приведена на рис. 1. Если температура в помещении превышает температуру, заданную оператором, то контроллер подает управляющий сигнал на закрытие клапана в сторону источника теплоснабжения и открытие на перемычку. В холодный период года устанавливается нижний предел закрытия клапана в пределах 3–7 % от максимального, чтобы не допустить замораживания калорифера.
При понижении температуры в помещении подается сигнал на уменьшение расхода воды по перемычке и увеличение от теплоисточника. Для аналитического рассмотрения процессов в помещении, системе В и КВ и САУ воспользуемся методом передаточных функций [4]. Структурная схема САУ для этого случая показанана рис. 2.
Входом служит тепловое воздействие на помещение Q, Вт, выходом — отклонение температуры в помещении от уставки T, К. Система В и КВ и ее САУ играют роль отрицательной обратной связи. Тогда эквивалентная передаточная функция будет иметь смысл комплексного образа удельного отклонения температуры в помещении, К/Вт, при единичном тепловом воздействии.
Датчик, помещение и теплообменник с достаточной точностью описываются как линейные позиционные инерционные звенья 1-го порядка. При этом, имея в виду краткосрочность рассматриваемых процессов регулирования (порядка десятков секунд или нескольких минут), при определении коэффициента передачи kп и постоянной времени Tп помещения учитываются только его объем V,м3, вентиляционный воздухообмен L,м3/с, и показатель теплообмена на внутренних поверхностях αF, Вт/К, т.к. за рассматриваемое время тепловая волна не проникает вглубь ограждений [5]. Тогда передаточная функция помещения будет иметь вид:
Wп = kп/(tп × р +1), К/Вт, где kп =1/(αF + L × c ×ρ), К/Вт, (1)
Tп = V × c ×ρ/(αF + L × c ×ρ), с.
Здесь с — удельная теплоемкость воздуха помещения, Дж/(кг•К), ρ— его плотность, кг/м3, р, с–1 — символ Хевисайда, т.е. комплексный образ времени после интегрального преобразования Лапласа-Карсона. Исполнительный механизм считается линейным интегрирующим, а рабочий орган — линейным позиционным звеном, инерцией которых можно пренебречь. Передаточная функция регулятора принимается в зависимости от используемого закона регулирования. В самом общем случае, для ПИД-закона можно записать:
Wрег = kр × [1+1/(tиз × р) + Tпр × р], (2)
где kр — коэффициент передачи регулятора от датчика к исполнительному механизму, В–1, Tпр — время предварения, Tиз — время изодрома, с. Функции для остальных законов регулирования можно получить из уравнения (2) путем принятия Tпр = 0 и (или) Tиз→∞. В этом случае эквивалентная передаточная функция системы будет иметь вид [4]:
Wсист = Wn/(1+ Wд × Wрег × Wим × Wро × Wто × Wп). (3)
Возьмем помещение, для которого: kп = 0,001 К/Вт, τп = 1206 с, Wп = 0,001/(1206 × p +1).
Тогда для различных законов регулирования переходные функции системы, получаемые из (3) обратным преобразованием Лапласа-Карсона по специальной программе для ЭВМ и представляющие собой зависимость удельного отклонения температуры в помещении Y, К/Вт, при единичном тепловом воздействии от времени τ, с, будут иметь вид, показанный на рис. 3, 4 и 5.
Во всех случаях было принято kр = 0,00002 × В–1, кроме того, время изодрома для ПИ-закона считалось равным 1 с, а время предварения для ПД-закона — 20,8 с, в соответствии с использованными характеристиками помещения и оборудования. Легко увидеть, что остаточное отклонение температуры в случае ПИ-регулирования равно нулю, а для регулирования без интегральной составляющей оно стремится к определенному пределу, зависящему от соотношения kп и kр.
При чисто пропорциональном регулировании это отклонение больше и достигается оно быстрее, чем при подключении дифференциальной компоненты. Данные выводы согласуются со сведениями, приведенными в [4], но здесь расчетная схема дополнена учетом характеристик обслуживаемого помещения. Таким образом, получена основа математической модели переходных процессов при регулировании систем В и КВ, использующая характеристики всех звеньев САУ.
В дальнейшем эта модель будет использована для анализа процессов при различных вариантах устройства звеньев и законах регулирования с целью получения инженерных рекомендаций по подбору регуляторов.

























