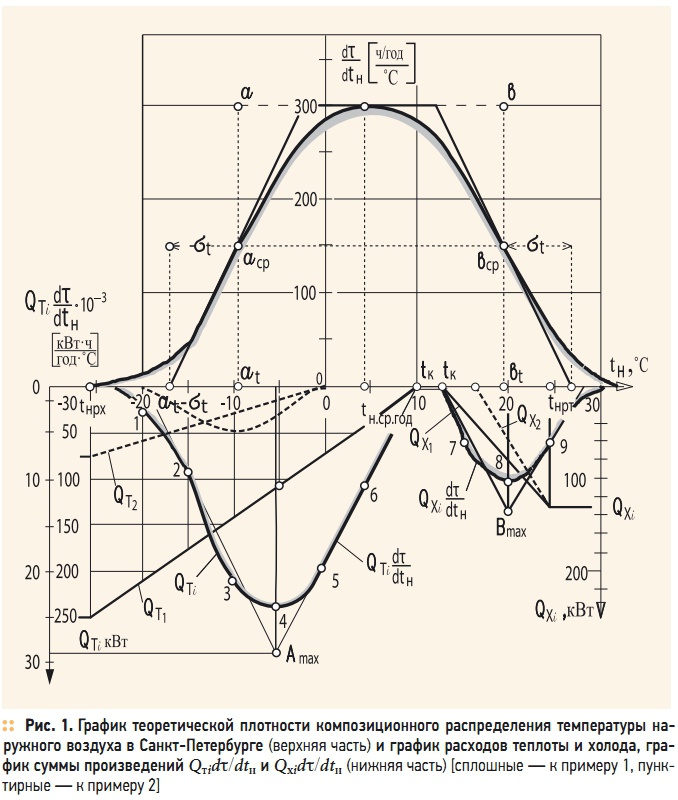
Рис. 1. График теоретической плотности композиционного распределения температуры на- ружного воздуха в Санкт-Петербурге (верхняя часть) и график расходов теплоты и холода, график суммы произведений Qтidτ/dtн и Qхidτ/dtн
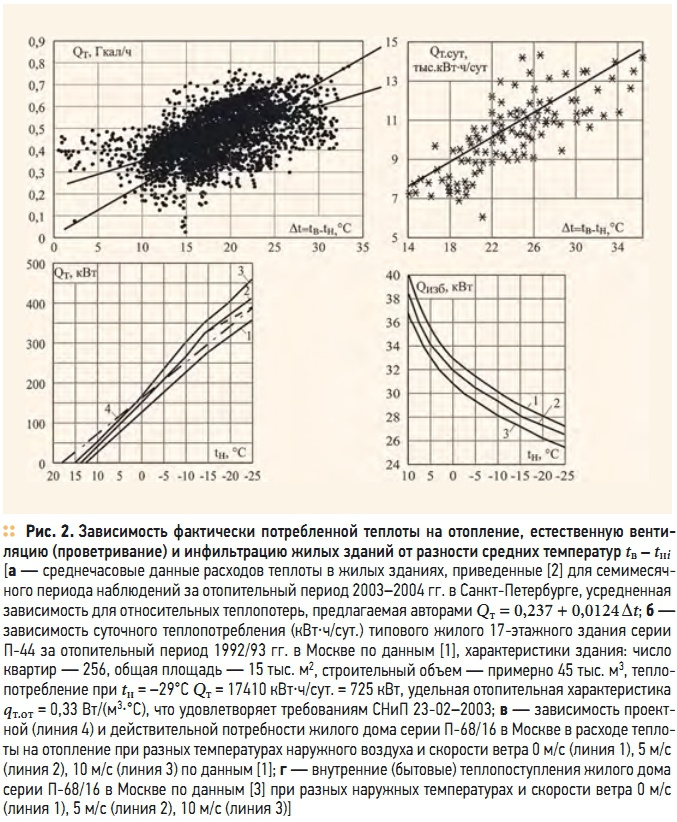
Рис. 2. Зависимость фактически потребленной теплоты на отопление, естественную вентиляцию (проветривание) и инфильтрацию жилых зданий от разности средних температур tв – tнi
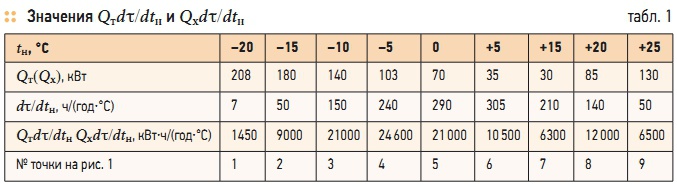
Табл. 1. Значения Qтdτ/dtн и Qхdτ/dt
16. В инженерных расчетах мне наиболее понятны те, которые сопровождаются графиками. Нигде не мог найти графоаналитической методики, объясняющей, как вычислить годовой расход теплоты и холода. Не могли ли Вы мне помочь в этом?
Методику привожу на примере, тогда она будет более понятной, предварительно сопроводив ее краткой теоретической частью. Графоаналитическая методика расчета основана на представлении годового расхода теплоты или холода интегралом (на графике это площадь, ее и определяют). В подынтегральном выражении (1) плотность повторяемости dτ/dtн или dτ/diн умножена на функцию текущего расхода теплоты Qт(tн) или холода Qх(tх) в зависимости от температуры или энтальпии наружного воздуха, например, так:
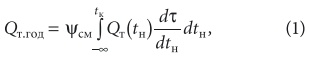
где плотность распределения описывается аналитически композиционным или приближенно-трапецеидальным законом. Для графических построений и соответствующего расчета проводят горизонтальную ось температуры или энтальпии наружного воздуха. Относительно нее по вертикальной оси в выбранном масштабе наносят линию — график плотности dτ/dtн в виде ступенчатой (эмпирической) или сглаженной линии и в другом масштабе — линию (обычно прямую) зависимости Qт(tн) или иную.
Последовательно перемножая величины dτ/dtн на Qт(tн) при нескольких значениях tн, например, –20 °C, –10 °C, 0 °C, 5 °C и выбрав новый масштаб произведения (dτ/dtн)Qт(tн), (ч/год)(кВт/°С), строят кривую, прижимающуюся на краях к оси tн. Заменяя площадь между этой кривой и горизонтальной осью равновеликим треугольником или трапецией, определяют по известным формулам геометрии ее площадь, которая численно равна искомому годовому расходу теплоты или холода в (кВт⋅ч)/год.
При определенном навыке такие построения и вычисления производят быстро, а сам метод отличается простотой и наглядностью. Поясним методику расчета годового расхода теплоты и холода центральной СКВ примером.
Пример 1. Определить графоаналитическим методом годовые расходы теплоты и холода для нагревания и охлаждения наружного воздуха в центральной СКВ без увлажнения в климатических условиях Санкт-Петербурга. Расчетный расход теплоты на нагревание наружного воздуха tн = tнрх = –26 °C до tк = 10 °С при его расходе Gпp = Gн = 7 кг/с составляет Qт.расч = 250 кВт, а расчетный расход холода на охлаждение наружного воздуха при увеличенном его расходе и охлаждении от tн = 25 °С до tк1 = 13 °С Qх.расч = 130 кВт.
Для расчета использовать композиционное распределение температуры наружного воздуха, а для сравнения провести расчет теплоты на нагревание по данным СНиП 2301–99 при продолжительности периода τtн < 10 °C = 239 сут/год = 5740 ч/годи средней температуре этого периода tн.cp = –0,9 °C. Режим работы системы принять непрерывным (ψсм = 1,0).По карте рис. 7.1.8а [4] и известным географическим координатам Санкт-Петербурга (60° с.ш., 30,5° в.д.) определяем параметры композиционного распределения температуры наружного воздуха: at = –9,4 °C, bt = 19,3 °C, σt = 7,5 °C.
По этим трем параметрам поочередно строим сначала четырехугольник распределения, после этого — равновеликую ему трапецию, а затем, после ее сглаживания, композиционное распределение температуры dτ/dtн = f(tн).Сначала проведем горизонтальную ось температуры наружного воздуха (рис. 1)и проставим на ней в выбранном масштабе значения tн = –30 °C, –20 °C, –10 °С … +30 °С.
Укажем на этой оси расчетные температуры наружного воздуха tнрх = –26 °С, tнрт + Δtпр = 25 °С, конечную температуру нагрева tк = 10 °C и конечную температуру охлаждения tк1 = 13 °C. Кроме этого, нанесем на этой оси точки с температурами tн = at = –9,4 °С и tн = bt = 19,3 °С. Вычислим максимальную плотность повторяемости этого распределения [ч/(год⋅°C)]:
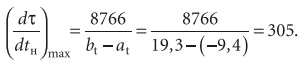
Эту величину в выбранном масштабе отложим на вертикальной оси dτ/dtн. Заменим прямоугольник atabbt равновеликой трапецией с основанием bt – at + 2σt и той же высотой (рис. 1). После этого скруглим склоны трапеции, оставляя неизменным положение ее точек acp и bcp на середине высоты, в результате будет построена плавная кривая:
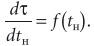
В нижней части графика проведем вертикальную ось тепловой Qт и холодильной Qх нагрузки системы. Поскольку эти величины одного порядка, то их масштаб примем одинаковым. Проводим прямую линию Qт при условии, что при tн = tк = 10 °С Qт = 0, а при tн = tнрх = –26 °С Qт = 250 кВт. Аналогично проводим прямую линию Qх при условии, что при tн = tк1 = 13 °С Qх = 0, а при tн = tнрт = 25 °С Qт = 130 кВт.
При более высоких температурах, чем tнрт = 25 °С, расход холода не может быть увеличен, и поэтому на графике Qх(tн) в этой точке имеется перелом. Выберем несколько значений температуры tн, для них определим соответствующие значения Qт и Qх, а также плотность повторяемости dτ/dtн, перемножим эти величины, а их произведение Qтdτ/dtн и Qхdτ/dtнзапишем в табл. 1. По результатам вычисления произведений в выбранном масштабе, с учетом того, что:
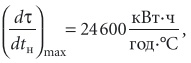
выбираем дополнительную ось этой величины и ставим точки 1, 2, 3, … 9 соответственно температурам в табл. 1. После этого заменим площадь между кривой по точкам 1, 2, … 6 и горизонтальной осью температур равновеликим треугольником с основанием Δtн = 10 – (–20) = 30 °С, вершиной в точке Amax, высотой этого треугольника Qтdτ/dtн = 29 × 103 кВт⋅ч/(год⋅°С). Искомый годовой расход теплоты на нагревание наружного воздуха соответствует площади данного треугольника и составляет 0,435 млн кВт⋅ч/год:
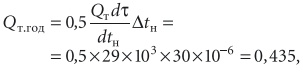
Для проверки этой методики и сравнения с данными СНиП 2301–99 определим годовой расход теплоты по следующей формуле и получаем результат 0,44 млн кВт⋅ч/год:Qт.год ≈ Gпрcв(tк – tн.cp)τнагр = = 7 × 1 × 5740[10 – (–0,9)] × 10–6 = 0,44.Как следует из результатов сравнения расчетов по двум методикам, искомые годовые расходы оказались практически одинаковыми.
В меньшем интервале температур нагреваемого воздуха сравнительная погрешность расчета по разным методикам возрастает. Аналогично вышеописанному, определим годовой расход холода на охлаждение наружного воздуха в теплый период года. Для этого заменим площадь между кривой, построенной через точки 7, 8 и 9, и горизонтальной осью температур равновеликим треугольником с основанием Δtн = 28 – 13 = 15 °С, вершиной в точке Bmax, высотой этого треугольника Qхdτ/dtн = 13,5 × 103 кВт⋅ч/(год⋅°С).
Искомый годовой расход холода на охлаждение наружного воздуха соответствует площади треугольника с указанным основанием и высотой и составляет 0,1 млн кВт⋅ч/год:
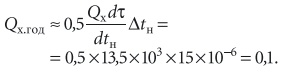
17. Объясните, как по этой методике определить годовой расход теплоты системы вентиляции после ряда теплосберегающих мероприятий и сравнить с первоначальным?
Для сравнения вычисленного годового расхода теплоты в СКВ без теплосберегающих мероприятий с расходом теплоты в такой же системе, но после ряда энергосберегающих мероприятий приведем нижеследующий пример в продолжение предыдущего.
Пример 2. Определить уменьшенный годовой расход теплоты на нагрев наружного воздуха в СКВ в условиях примера 1 после комплекса следующих теплосберегающих мероприятий:
- естественная приточная (при наличии в окнах открывающихся фрамуг и подаче воздуха в направлении перекрытия) и вытяжная механическая вентиляция помещения в интервале температур наружного воздуха tн = 0–17 °С;
- утилизация теплоты удаляемого воздуха при средней эффективности процесса θту = 0,7, что сокращает расчетный расход теплоты (рис. 1)с Qт.расч = 250 кВт доQт.расч1 = (1 – θту)Qт.расч = (1 – 0,70) × 250 = 75 кВт.
На графике рис. 1 пунктиром проводим линию текущих расходов теплоты Qт2 и холода Qх2 в такой системе при условии, что при tн = 0 °С Qт = 0, при tнрх = –26 °С Qт.расч = 75 кВт, соответственно, при tн = 17 °С Qх = 0, при tнрт = 24,6 °С Qх.расч = 130 кВт. Умножением частных значений Qтi и dτ/dtн при нескольких наружных температурах tн = –2,5 °С, –5 °С, –10 °С получаем новые значения произведения Qтidτ/dtн (пунктир). Заменяя эту кривую равновеликой трапецией, получаем уменьшенный годовой расход теплоты Qт.год = 5 × 103 × 13,5 × 10–3 = 67 тыс. кВт⋅ч/год, что в 6,7 раз меньше ранее вычисленного расхода теплоты аналогичной СКВ, но без теплосберегающих мероприятий.
18. Мне непонятно, чем отличаются вычисленные теплопотери помещений и зданий от фактической нагрузки на системы отопления? К тому же постоянное обсуждение путей снижения тепловой нагрузки на отопление мне кажется однообразным и не содержащим ничего нового. Прав ли я?
Отопительная нагрузка здания складывается из основных и добавочных теплопотерь, теплоты, затрачиваемой на инфильтрацию и периодическую вентиляцию (проветривание), нагрев ввозимых материалов и др. При кажущейся внешней простоте отопительная нагрузка помещения и здания далеко не однозначна в своем определении и зависит, с одной стороны, от внешних климатических условий (температуры наружного воздуха, направления и скорости ветра, солнечной радиации), а с другой стороны — от теплозащитных свойств наружных ограждений, площади и негерметичности светопроемов, инфильтрации, режима проветривания помещений, управления системой отопления и других факторов.
Обсуждая теплопотери здания и их зависимость от наружной температуры, обычно упрощенно линеаризуют функцию Qтп = f(tв – tнi), пренебрегая всеми остальными факторами и сложными климатическими воздействиями. В свете давно известного и физически объяснимого разделения теплопотерь на быстрые (через окна) и медленные (через непрозрачные ограждения), описанного, например, С.А. Чистовичем [6–8] и использованного автором (А. Сотников) для решения задач отопления [5], а также с учетом хаотичной радиации становится понятной сложность изучаемых процессов.
Поэтому мы приходим к другому, более тонкому и точному толкованию анализируемого явления. Здесь, несомненно, имеет место многофакторность и частотная модуляция воздействий, когда годичный ход температуры tн(τ) может быть представлен гармоникой и неупорядоченными на разных частотах колебаниями температуры, скорости и направления ветра, солнечной радиации.
При таком беспорядке и неопределенности ответа отопления (управляемого или неуправляемого) становится понятной стохастичность точек на рис. 2а, б, в других источниках. На практике неоднократно описывали и фактически наблюдали это многофакторное явление. Как пример этих зависимостей, на рис. 2а–г приведены опытные данные, многократно отмеченные и зарегистрированные в разные годы в жилых зданиях по показаниям счетчиков-тепломеров, по данным и публикациям А.Н. Сканави и Л.М. Махова [3], Ю.А. Матросова, И.Н. Бутовского и Д. Гольдштейна [1], В.А. Пухкала и Л.Р. Крумера [2] и др.
Как общий вывод авторы статей [1, 2, 3, 6–8 и др.] подчеркивают сложный характер зависимости фактически наблюдаемых расходов теплоты на отопление жилых зданий от разности Δt = tв – tн. Опытные значения образуют на графиках поле точек, поэтому зависимость теплопотерь от разности температур далека от линейной. В частности, при малых перепадах температур tв – tн < 15 °С и достаточном отпуске теплоты в здании при открывании окон и форточек воздухообмен увеличивается до величины, не нарушающей тепловой комфорт человека.
Расход теплоты на отопление и естественную вентиляцию в этом случае остается практически постоянным и значительно превышает проектное значение. При перепадах температур tв – tн > 25 °С наблюдается снижение теплопотребления по сравнению с проектными данными из-за срезки температурного графика на источнике теплоты и уменьшения естественного проветривания.
Как общий вывод и результирующий ответ на ваши вопросы, отмечу, что очень сложно разобраться в совокупности упорядоченных и хаотичных воздействий на здания, формирующих его потребность в теплоте в данный момент, а тем более за год. В результате т.н. «простое отопление» является далеко не простым в энергопотреблении и энергосбережении.


























