Утилизация теплоты в перекрестно-точных пластинчатых рекуператорах

Расчет данных теплообменников обычно проводится с использованием укрупненных показателей инженерными методами, в основе которых лежат упрощенные схемы тепломассопереноса. Ряд грубых схематизаций реальных процессов ведет к неточностям при расчетах и значительно ограничивает возможности проектанта по совершенствованию режимных и конструктивных параметров. Автором предложена уточненная методика расчета перекрестно-точных пластинчатых рекуператоров, основанная на фундаментальных законах сохранения энергии, движения и массы [1, 2].

Данные о распределении температур приточного и удаляемого воздуха могут быть получены из решения системы дифференциальных уравнений в частных производных:

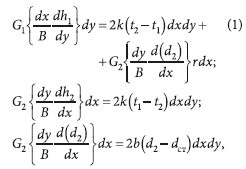
где В — ширина (длина) пластины теплообменного пакета; d2 — влагосодержание удаляемого воздуха; dст — влагосодержание, соответствующее насыщению при температуре стенки; G1, G2 — массовые расходы приточного и удаляемого воздуха; h1, h2 — средние по высоте каналов энтальпии приточного и удаляемого воздуха; t1, t2 — текущие температуры приточного и удаляемого воздуха; x, y — продольная и поперечная координаты; k — коэффициент теплопередачи; b — коэффициент массообмена. Сопоставление расчетных данных с экспериментальными показали хорошее согласование теории и опыта [3].



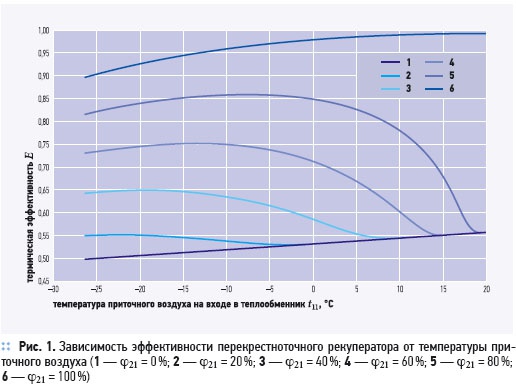
Зависимость эффективности перекрестно-точных рекуператоров от температуры приточного воздуха
На основе анализа расчетных полей температур и влагосодержаний можно получить зависимости, определяющие эффективность рекуператора от влажности, температур, расходов воздуха и геометрии теплообменного пакета. Особый интерес представляет зависимость эффективности рекуператора от температуры приточного воздуха. Ниже в качестве примера представлены расчеты для пластинчатого перекрестно-точного рекуператора с теплообменным пакетом 350 × 350 × 350 мм при расходе притока и вытяжки 350 м3/ч в интервале температур приточного воздуха –26…+22 °C.

При расчетах неизменными приняты следующие величины: температура удаляемого воздуха t21 = 22 °C; влажность приточного воздуха 𗼿 = 75 %.Термическую эффективность как правило определяют по формуле (равные расходы притока и вытяжки):

где t11, t12 — температуры приточного воздуха на входе и на выходе из теплообменника; t21 — температура удаляемого воздуха на входе в теплообменник.

Числитель дроби можно рассматривать как характеристику рекуператора, т.е. степень совершенства теплообмена, определяемая в основном конструктивными особенностями теплообменника. Знаменатель представляет фактическую разность температур приточного и удаляемого воздуха на входе в теплообменник, которая может принимать любые значения из заданного интервала.



Из рис. 1 (кривая 1) видно, что по мере снижения температуры приточного воздуха термическая эффективность рекуператора убывает. Данное явления связано с тем, что степень утилизации теплоты удаляемого воздуха, или степень нагрева приточного воздуха, и разница температур потоков на входе в теплообменный пакет возрастают неравномерно. Рост разницы температур потоков на входе t21 – t11, очевидно, опережает возрастание степени нагрева приточного воздуха t12 – t11. Для обеспечения равной эффективности при больших градиентах температуры рекуператор должен иметь более развитую поверхность теплообмена. Из (2) следует, что эффективность будет снижаться по мере убывания температуры приточного воздуха, что видно на примере хода кривой эффективности при условиях сухого теплообмена (𗽉 = 0 %, кривая 1).



В том случае, если удаляемый воздух является влажным, охлаждение до температуры ниже точки росы влечет за собой конденсацию водяного пара. Теплота конденсации передается приточному воздуху, в итоге повышая температуру последнего на выходе из пакета. Из характера зависимостей 2–6 (рис. 1) видно, что термическая эффективность рекуператора начинает возрастать с уменьшением температуры приточного воздуха в тот момент, когда начинается образование конденсата, что соответствует достижению стенкой температуры насыщения. По мере того, как все больше пара выделяется из удаляемого воздуха, эффективность продолжает увеличиваться, достигает максимума при некоторой температуре, а затем начинает убывать. Данное снижение эффективности рекуператора объясняется тем, что содержание водяного пара во влажном воздухе описывается нелинейной зависимостью, и чем ниже температура паровоздушной смеси, тем меньшее количество пара переходит в жидкую фазу при охлаждении воздуха на один градус. В результате, приточный воздух нагревается в меньшей степени.



Данный факт наглядно отображается зависимостью 6 (рис. 1): при подаче в теплообменник удаляемого влажного воздуха, который находится в насыщенном состоянии, термическая эффективность рекуператора убывает при снижении температуры приточного воздуха аналогично случаю подачи абсолютно сухого воздуха. Видимо, качественный характер зависимости эффективности от температуры приточного воздуха, полученный для данного примера, является общим для всех перекрестно-точных рекуператоров.

Режим работы рекуператоров в при температурах приточного воздуха ниже –10…–5 °C следует рассматривать как критический, поскольку в этом случае возможно образование инея в каналах, что приводит к росту аэродинамического сопротивления теплообменного пакета и, как следствие, деградации теплообмена вплоть до выхода системы из строя. На основе накопленного экспериментального материала можно утверждать, что именно образование инея в каналах, а не замерзание жидкого конденсата представляет основную проблему при эксплуатации рекуператоров в области низких температур.



Оптимизация конструкции перекрестно-точного рекуператора
Необходимость решения задачи оптимизации режимных параметров и конструкции перекрестно-точных рекуператоров возникает в результате того, что любое изменение геометрии и режима работы неоднозначно сказывается на таких показателях как аэродинамическое сопротивление, стоимость теплообменника и эффективность. Так, возрастание эффективности может сопровождаться ростом падения давления в пакете и увеличением стоимости теплообменника.



В связи с этим оптимизационная задача — многоцелевая, т.к. выбор лучшего варианта требует учета большого количества факторов. Наряду с отсутствием вычислительных проблем поиска экстремума нескольких целевых функций, которые слагают многокритериальный или векторный показатель качества установки, существуют некоторые методологические трудности поиска альтернативы. Частными целевыми функциями в рассматриваемом случае являются: эффективность, потери давления в рекуператоре и стоимость пакета. Многокритериальную оптимизацию рационально проводить в скалярной постановке с использованием метода «справедливого компромисса».



Пусть каждый критерий di(u) характеризует некоторый оптимизируемый показатель изделия u. Лучший вариант характеризуется наиболее удачным сочетанием всех показателей качества. Многоцелевая задача, таким образом, сводится к поиску экстремума функции следующего вида


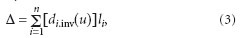
где li — коэффициент значимости iго показателя качества. Принимается, что:


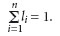
Значения li для каждой частной оценки выбирается на основе принятия экспертного решения. Строго регламентировать li невозможно, поскольку каждый теплообменник эксплуатируется в различных условиях и может быть изготовлен из различных материалов. Поэтому набор коэффициентов значимости оригинален для каждого конкретного случая. При равной значимости всех оценок имеем li = 1/n. Поскольку единицы измерения отдельных критериев различны, их приводят к инвариантному диапазону. Теплообменный пакет рекуператора характеризуется высотой пакета F, шириной (длиной) пакета В, высотой каналов Н. Задача оптимизации заключается в определении максимума глобальной функции качества и геометрии пакета, соответствующей экстремуму этой функции. Таким образом, используя формулу (3), глобальное качество можно представить в виде:


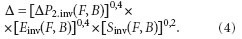
Показатели степени при частных инвариантных критериях дают в сумме 1. При выводе формулы (4) веса показателей получены из соображений о равной значимости эффективности и аэродинамического сопротивления и более низкой значимостью стоимости материалов (площади пластин).Отношение весов показателей степени при эффективности Е, сопротивлении ΔР2 и площади S составляет, соответственно, 1:1:0,5.

Исходные данные:
❏ температура удаляемого воздуха имеет величину t21 = 22 °C;
❏ влажность удаляемого воздуха имеет величину 𗽉 = 65 %;
❏ температура приточного воздуха имеет величину t11 = 0 °C;
❏ влажность приточного воздуха имеет величину 𗼿 = 75 %;
❏ номинальный расход имеет величину G1 = G2 = 350 м3/ч.

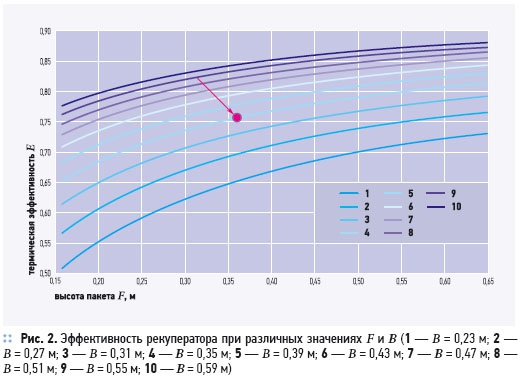
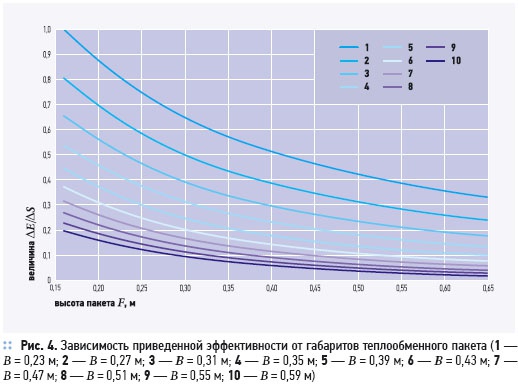
Результаты расчетов частных функций качества приведены на рис. 2–5. На рис. 2 представлена зависимость эффективности рекуператора от габаритов пакета. Можно видеть, что увеличение каждого из размеров F и B приводит к увеличению эффективности вследствие роста площади теплообмена и снижения массового расхода через отдельно взятую пластину. Возрастание эффективности наиболее интенсивно протекает в области малых размеров теплообменного пакета. Последнее объясняется особенностями распределения температур и коэффициентов теплоотдачи при перекрестном токе.


Стрелка на рис. 2 определяет эффективность, высоту пакета и ширину пластины базовой модели рекуператораF × B × B × H = 350 × 350 × 350 × 4 мм.

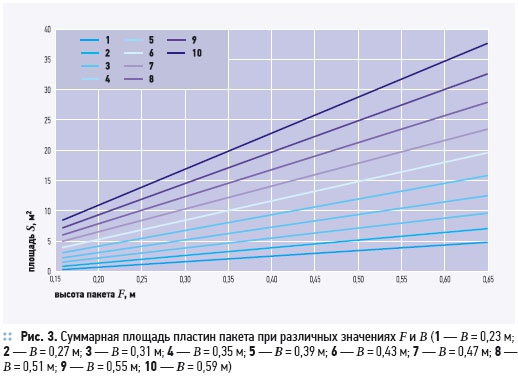
Используя представленные графики, можно определить эффективность рекуператора при фиксированном расходе для широкого диапазона размеров пакета. Так, эффективность базовой модели может быть достигнута при различных сочетаниях F и B; определить численные значения высоты и ширины пакета, соответствующие фиксированному значению эффективности, можно, смещаясь по горизонтали из исходной точки. На рис. 3 представлена зависимость площади теплообмена от высоты и ширины пластины пакета. Безразмерное приращение эффективности ΔЕ, отнесенное к безразмерному приращению площади ΔS определит приведенную эффективность. Приведенная эффективность зависит от абсолютной величины площади теплообмена и уменьшается по мере возрастания габаритов теплообменника, что показано на рис. 4.

В области малых значений F и B увеличение S приводит к более значительному увеличению эффективности, чем аналогичное приращение площади при больших значениях F и B. Этим объясняется асимптотический характер кривых 1–10 (рис. 4). Увеличение какого-либо из размеров крупногабаритного теплообменника слабо сказывается на изменении эффективности (кривая 10 на рис. 4) и влияет, в основном, на сопротивление рекуператора. Таким образом, можно говорить о существовании оптимального сочетания параметров F и B, соответствующего рациональной эффективности перекрестно-точных рекуператоров, превышение которой за счет увеличения габаритов установки влечет за собой существенное удорожание конструкции.

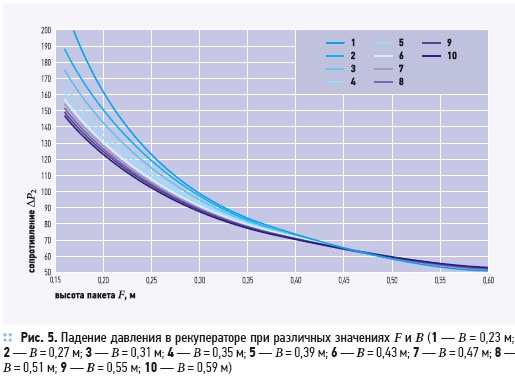
На рис. 5 приведены кривые зависимости падения давления в рекуператоре от габаритов пакета. Анализ представленных графиков позволяет сделать заключение, что изменение высоты пакета F значительно сильнее сказывается на сопротивлении пакета, чем изменение параметра B. Таким образом, при совершенствовании конструкции с целью снижения потерь давления в теплообменнике, следует отдавать предпочтение именно увеличению высоты пакета F.

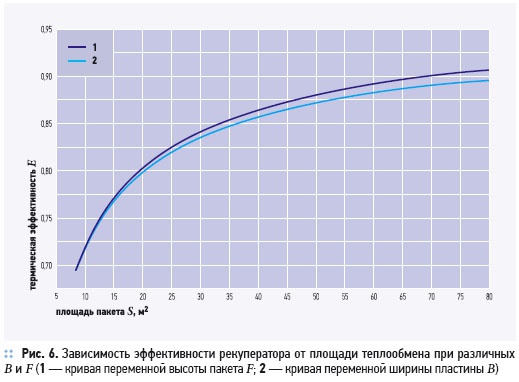
Одна и та же площадь теплообменной поверхности может быть получена при различных сочетаниях F и B. Интерес представляет зависимость эффективности и падения давления в рекуператоре от площади теплообменной поверхности.

Приращение площади S может быть достигнуто двумя путями: при фиксированной высоте пакета F — увеличением ширины пластины B, при фиксированном В — увеличением высоты F. Неизменные геометрические параметры соответствуют размерам базовой модели, расходы — номинальному значению. Результаты приведены на рис. 6 и 7. Как следует из рис. 6, эффективность рекуператора возрастает при увеличении S, причем возрастание высоты пакета (кривая 1) приводит к более высоким значениям эффективности, чем увеличение ширины пластины пакета (кривая 2). Отсюда следует, что степень утилизации теплоты в рекуператоре в большей степени определяется расходом теплоносителей и в меньшей степени — площадью отдельно взятой пластины. Однако разность эффективности для двух рассмотренных случаев незначительна и не превышает нескольких процентов.

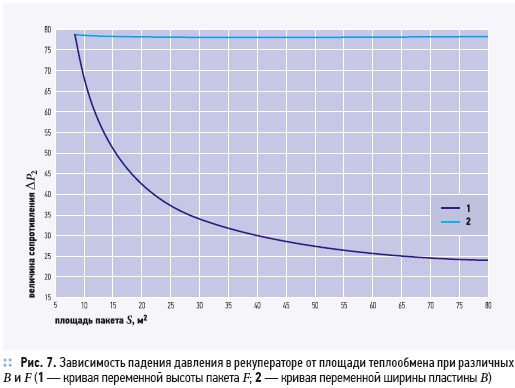
На рис. 7 представлена зависимость падения давления от площади поверхности теплообмена. Можно видеть, что увеличение F (см. также рис. 5) значительно уменьшает сопротивление рекуператора вследствие существенного снижения скорости течения в каналах пакета при неизменной длине канала и ширине пластины (B = const). Последнее, приводит к уменьшению потерь давления на трение в теплообменном пакете. Изменение B незначительно сказывается на величине ΔР2 (кривая 2, рис. 7). В области малых значений B имеет место снижение потерь давления, в области больших B — слабое увеличение (не отражено в масштабе графика), вызванное ростом потерь на удар на входе и выходе из рекуператора в патрубки. Описанная слабая зависимость ΔР2(В) обусловлена тем фактом, что снижение скорости течения в пакете (как результат увеличения живого сечения) компенсируется увеличением длины каналов.

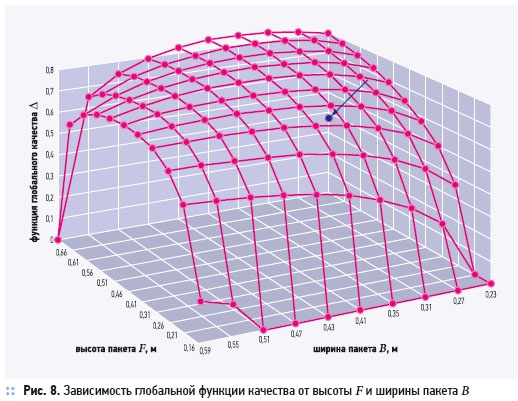
Объединяя частные критерии качества в глобальную функцию в соответствии с (4), получим зависимость качества рекуператора в виде поверхности в поле параметров F и B (рис. 8). Стрелкой на рисунке указано качество базовой модели. Оптимальному качеству соответствует максимум функции Δ(F, B), т.е. вершина поверхности.

Оптимальное отношение F/B лежит в пределах 1,6–2,0. Таким образом, теплообменный пакет с лучшим сочетанием эксплуатационных и стоимостных показателей имеет вид параллелепипеда, набранного из значительного количества пластин небольшой площади.

Использование h–d-диаграммы для анализа процессов утилизации в перекрестно-точных рекуператорах
Большинство перекрестно-точных теплообменников изготавливается из непроницаемых для водяного пара и конденсата материалов. Проведем теоретическое исследование возможности утилизации потенциала удаляемого воздуха в пластинчатом рекуператоре с непроницаемыми стенками.

Выражение для энтальпии влажного воздуха при t > 0 °C имеет вид:

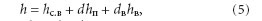
где hc.в, hп, hв — удельные энтальпии сухого воздуха, водяного пара и воды; dв — массовое содержание воды (водность). Подставляя в уравнение значения удельных энтальпий сухого воздуха, пара и воды, получаем:


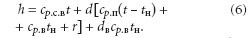
где cр.с.в, cр.п, cр.в — средние изобар-ные теплоемкости сухого воздуха; пара и воды; tн — температура насыщения; r — теплота парообразования. Последний член формулы (6) — эн-тальпия содержащейся в воздухе воды. На основе (6) можно получить выражение для определения энтальпий влажного воздуха в состоянии насыщения, тумана, а также вычислить изменение энтальпии при охлаждении. В том случае, если воздух является ненасыщенным, из (2) следует, что энтальпия:


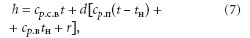
для насыщенного воздуха:


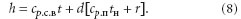
В формулах (7)–(8) член dвcр.в отсутствует, поскольку содержание воды в системе равно нулю. При охлаждении ненасыщенного влажного воздуха до температуры, выше точки росы изменение влагосодержания не происходит, и разность энтальпий запишется в виде:


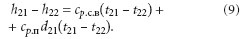
Охлаждение ненасыщенного влаж-ного воздуха ниже точки росы сопрово-ждается изменением энтальпии:


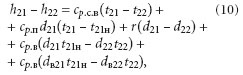
где t21н — температура точки росы влажного воздуха с параметрами d21, t21 (температура насыщения). Параметры d22, t22 соответствуют состоянию насыщения (индекс «н» опущен). Заметим, что dв21 = 0, т.к. в начале охлаждения в воздухе отсутствует жидкая фаза. Содержание воды в системе в конце процесса dв22 = d21 – d22. Формула (10) преобразуется в следующим образом:


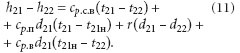
В рекуперативных теплообменниках при отсутствии массообмена между потоками наиболее полно потенциал удаляемого воздуха можно использовать, охладив его до начальной температуры приточного, т.е. t22 = t11. Вследствие того, что влажный приточный воздух в большинстве случаев является ненасыщенным, равенство температур t22 = t11 не обеспечивает равенства энтальпий h22 и h11. Для более подробного рассмо-трения процесса охлаждения влажно-го воздуха, обратимся к h–d-диаграмме (рис. 9).

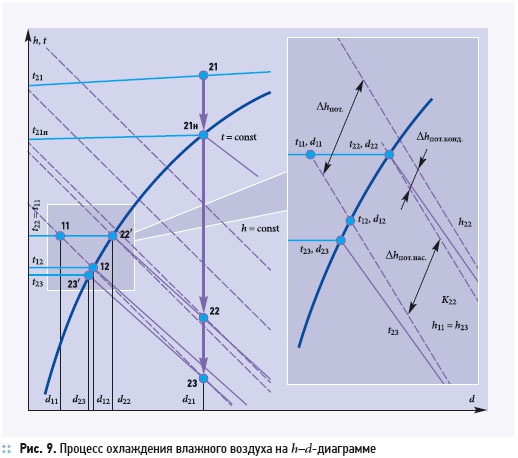
Охлаждение влажного воздуха от t21 до t22 = t11 изображается на диаграмме прямой, соединяющей точки 21 и 22, и проходит два этапа: первый — охлаждение ненасыщенного воздуха до тем-пературы точки росы t21н; второй — охлаждение насыщенного воздуха до состояния точки 22, сопровождающееся переходом в область водяного тумана. Параметры состояния насыщенно-го водяного пара в конце процесса охла-ждения t22, d22 определяются точкой 22, лежащей на линии насыщения. Так как изотермы в области тумана не парал-лельны линиям постоянного теплосодержания, энтальпия влажного возду-ха h22 оказывается выше, чем энтальпия, соответствующая состоянию точки 22ʹ. Графически значение энтальпии h22 можно получить, определив точку пересечения изотермы t11 и линии постоянного влагосодержания 21–22. Потенциал, удаляемого влажного воздуха, который не может быть утилизирован в рекуператоре с непроницаемыми стенками, обозначим Δhпот. Разница энтальпий удаляемого и приточного воздуха на входе в теплообменник определяется из уравнения:


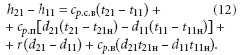
Изменение энтальпии удаляемого воздуха при охлаждении до t22 = t11 определяется из уравнения (11). Вычитая (11) из (12) получаем величину, характеризующую энтальпию, которая не может быть утилизирована в теплообменнике:


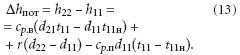
Потерь энтальпии в рекуператоре нельзя избежать даже в том случае, когда приточный воздух находится в насыщенном состоянии. Пусть параметры приточного воздуха d22, t22 определяются точкой 22ʹ (1). Энтальпия удаляемого влажного воздуха в конце процесса охлаждения определяется, как:


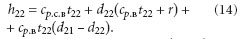
Учитывая то, что t22 = t22, d22 = d22, потери энтальпии составят:


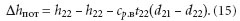
Нетрудно видеть, что Δhпот обусловле-но наличием в удаляемом воздухе скон-денсировавшегося водяного пара, при-чем величина потерь равна энтальпии жидкой фазы. Последнее объясняет тот факт, что на рис. 9 изоэнтальпа h22 лежит выше h22. Преобразуем выражение для суммарных потерь энтальпии (13):


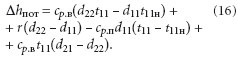
Первые три члена представляют разницу энтальпий двух состояний приточного воздуха, соответствующих точкам 11 и 22ʹ, т.е. определяют увеличение энтальпии при переходе ненасыщенного влажного воздуха в состояние насыщения при неизменной температуре t11.Обозначим потери, вызванные присутствием конденсата Δhконд.пот, а разность энтальпий ненасыщенного воздуха и воздуха в состоянии насыщения при неизменной температуре — Δhнас.пот.

Тогда формулу (16) можно представить в следующем виде


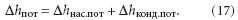
Если приточный воздух находится в насыщенном состоянии, то величина потерь, как сказано выше, определяется только энтальпией конденсата:


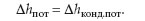
Так как энтальпия является функцией состояния, то ее изменение не зависит от выбранного пути интегрирования. Иными словами, переход из состояния точки 11 в состояние точки 22ʹ можно осуществить различными способами, при этом разность энтальпий h22 – h11 остается неизменной. Следовательно, формулу (16) можно записать в значительно более простом виде


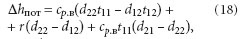
,где t12, d12 — температура и влагосодержание приточного воздуха, соответствующее состоянию насыщения при энтальпии h11. Очевидно, состояние влажного воздуха в точке 12 определяется показанием смоченного термометра. Первые два члена (18) представляют собой разность энтальпий насыщенного воздуха состояния 22ʹ (t11 = const) и насыщенного воздуха состояния 12 (h11 = const) и изображается на диаграмме отрезком длиной Δhнас.пот.

Утилизация потенциала вентвыбросов может быть полной, если обеспечивается равенство энтальпий удаляемого влажного воздуха в конце охлаждения и энтальпии воздуха, поступающего из окружающей среды. Продолжая линию 21–22 ниже до пересечения с изоэнтальпой h11 = const, получаем точку 23. Поднимаясь по изотерме h23 = const до пересечения с кривой насыщения, находим точку 23ʹ, состояние насыщенного воздуха в которой определяется температурой и влагосодержанием t23, d23. Так как t23 < t11, переход 21–23 осуществить невозможно без обеспечения массообмена между теплоносителями.


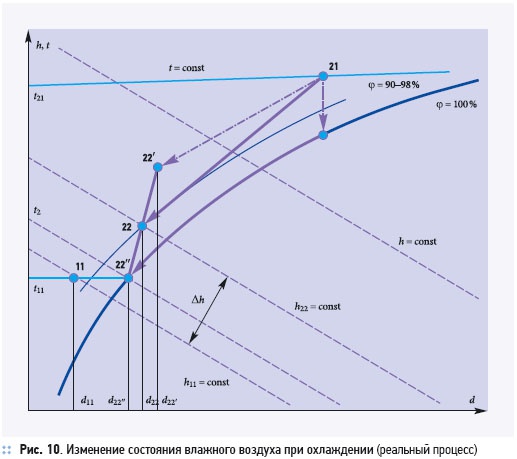
Рассмотренный выше процесс описывает идеальное охлаждение удаляемого воздуха и его предельное состояние в конце процесса, что может иметь место, к примеру, при теплообмене в длинных каналах, когда температура и влажность не изменяются ниже по течению и по высоте канала. Сложность отображения реальных процессов на h–d-диаграмме заключается в том, что в классической термодинамике (на основании законов которой построена диаграмма Молье) рассматриваются равновесные системы со средними по объему параметрами состояния. При внутреннем течении влажного воздуха с охлаждением и конденсацией водяного пара области, прилегающие к стенке, имеют более низкую температуру, чем области в районе оси канала (ядро течения). В теплообменном пакете рекуператора градиенты температур и концентраций пара существуют не только в плоскости пластин, но и в вертикальных сечениях каналов. Диффузия водяных паров от центра к периферии (стенке) приводит к осушению воздуха в ядре течения, поэтому здесь не наблюдается переход воздуха в насыщенное состояние. У стенок, напротив, наблюдаются значительные пересыщения. Реальный процесс охлаждения влажного воздуха, таким образом, будет протекать вдоль линии 21–22 (рис. 10). При этом изменение состояния воздуха в центре канала описывается прямой 21–22ʹ, а изменение его состояния у периферии — прямой 21–22ʺ.Результирующее значение температуры и влагосодержания t22, d22 определяется как интеграл по высоте канала, или упрощенно, как среднее от величин t𑁚, t𑂾, d𑁚, d𑂾. В результате, конечная относительная влажность будет лежать в пределах 90–98 %, что соответствует рекомендациям по расчетам поверхностных воздухоохладителей. Количество теплоты, которое теряется в данном теплообменнике, определится отрезком Δh.

1. Белоногов Н.В., Пронин В.А. Математическое моделирование процессов теплообмена в перекрестно-точном пластинчатом рекуператоре // Вестник МАХ, №4/2003.
2. Белоногов Н.В., Пронин В.А. Расчет эффективности перекрестно-точных пластинчатых теплообменников // Вестник МАХ, №4/2004.
3. Белоногов Н.В., Пронин В.А. Экспериментальное исследование теплообмена в перекрестно-точном пластинчатом рекуператоре // Известия СПбГУНиПТ, №1/2004.
4. Хаузен Х. Теплопередача при противотоке, прямотоке и перекрестном токе: Пер. с нем. — М.: Энергоиздат, 1981.