Баки-гидроаккумуляторы (гидропневматические баки, гидробаки, мембранные баки и т. п.) широко используются в небольших системах водоснабжения, как на первом, так и на втором подъёмах. На первом подъёме бак-гидроаккумулятор выполняет обычно функцию сглаживания гидравлических ударов при пуске и остановке насоса (как правило, это погружной насос водозаборной скважины). Особенности работы гидроаккумулятора для такого случая рассматривались в [1].
На втором подъёме гидроаккумулятор является по сути напорно-регулирующей ёмкостью, позволяющей создать некоторый объём воды под давлением. За счёт этого объёма обеспечиваются небольшие расходы воды, что особенно важно при значительной неравномерности водопотребления. Также обеспечивается компенсация утечек воды, возникающих вследствие неплотностей в трубопроводах и водопроводном оборудовании, без включения подающего насоса возможно более продолжительное время. Баки могут устанавливаться и на «прямоточных» схемах водоснабжения, когда погружной насос скважины подаёт воду непосредственно водопотребителям — с системой очистки воды или без неё.

Подбор бака-гидроаккумулятора сводится к расчёту его объёма. Сложность этой задачи заключается в учёте сочетания одновременного изменения объёма и давления газа (воздуха) и воды в герметично закрытом от атмосферы корпусе бака. Если даже говорится, что расчё- том определяется частота включения насоса, в любом случае речь идёт именно об определении того резервного, буферного рабочего объёма, который может использоваться, как уже было сказано, для компенсации небольших расходов воды (разумеется, сугубо ограниченное время) и утечек из системы водоснабжения.
Далее приведены несколько формул для расчёта объёма гидробака (они же были приведены и в [1]):
W = qhr sp.i/(4n), (1)
где qhr sp.i — часовой расход воды, подаваемой насосом; n — допустимое число включений насосной установки в час, для установок с гидропневматическим баком n = 6–10;
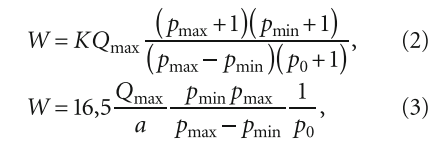
где Qmax — максимальный расход воды, л/мин.; pmax — максимальное давление, при котором насос отключается; pmin — минимальное давление, при котором насос включается; p0 — давление газа в гидроаккумуляторе; К — коэффициент, зависящий от мощности насоса; а — количество пусков системы в час.
Нетрудно заметить, что формула (1) избыточно упрощена — в ней даже не учитывается давление воды и воздуха. В формулы (2) и (3) входят значения верхнего pmax и нижнего pmin уровней давления воды в системе, давления воздуха внутри гидробака. При этом сложно оценить, на каких положениях основаны указанные формулы. Неясно, например, что означают коэффициенты 16,5 и К.
В частности, согласно пояснениям к уравнению (3), значение К тем больше, чем больше мощность подающего насоса: от К = 0,25 при мощности насоса 0,75–1,50 кВт до К = 0,875 при мощности 6,71–9,0 кВт. Можно признать логичным, что с ростом мощности насоса увеличивается и требуемый объём гидробака, но опять же неясно, на чем основана данная зависимость. По сути, формулы (2) и (3) в большей степени эмпирические.
Выражения (2) и (3) объединяет также то, что значения давления воды в них представлены в степени «1″, что предполагает протекание в воздушной подушке гидробака изотермического процесса, при котором теплообмен с окружающей средой при изменении объёма и давления происходит достаточно быстро, а температура остаётся практически постоянной.
Однако бак-гидроаккумулятор в силу своей конструкции является достаточно замкнутой системой, где получение теплоты извне и её отдача во внешнюю среду весьма затруднены, что позволяет считать его работу более близкой к другому газовому процессу — адиабатическому, при котором система практически не обменивается теплотой с окружающим пространством. Уравнение адиабатического процесса записывается как:
pWk = const, (4)
где k — показатель адиабаты, для сухого воздуха k = 1,4.
В сети Интернет можно встретить [2] следующее уравнение для расчёта объёма гидробака W на основе адиабатического процесса:
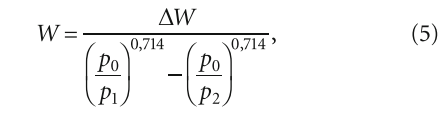
где p0 — давление газа; p1 — нижний уровень давления воды; p2 — верхний уровень давления воды; ΔW — объём аккумулируемой воды.
По мнению автора, выражение (5) достаточно адекватно описывает работу бака-гидроаккумулятора, но нуждается в некоторых поправках и разъяснениях. Например, что значит «объём аккумулируемой воды»? Или что понимать под объёмом гидробака W — полный объём бака, включая объём, заполненный воздухом, либо только объём, занятый водой? Возможно, именно вследствие не вполне понятных величин ΔW и W уравнение (5) и не нашло широкого распространения. Следовательно, прежде всего необходимо составить расчётную схему бака-гидроаккумулятора (рис. 1).
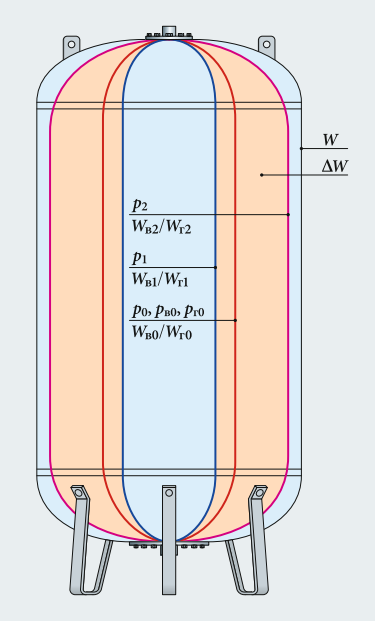
Рис. 1. Расчётная схема бака-гидроаккумулятора (объём воды, ограниченный p1, соответствует нижнему уровню давления; объём воды, ограниченный p2, соответствует верхнему уровню давления; объём воды, ограниченный p0, соответствует изначально созданному давлению воздуха p0 при равенстве с давлением воды pв0; ΔW — рабочий объём бака-гидроаккумулятора)
Как правило, давление газа (воздуха) в баке доводится до уровня 1,5–2 атм (чем больше объём бака, тем больше и устанавливаемое давление воздуха). Обозначим его pг0 — исходное давление газа (воздуха). Соответственно, и воздух при созданном изначально давлении pг0 займёт объём Wг0. Изначальные давление и объём воды обозначим как pв0 и Wв0. Поскольку давление отделённых друг от друга эластичной мембраной воздуха и воды в баке в любом случае одинаково, то pг0 = pв0 (далее будем именовать его как p0). В свою очередь, общий объём гидробака составит W = Wг0 + Wв0.

Здесь необходимо отметить, что соотношение Wг0 и Wв0 зависит от конструкции бака, которая задаётся производителем. По имеющимся у автора данным (со слов одного из производителей баков) оно составляет 1:1, то есть по 50% воды и воздуха, хотя, разумеется, оно может быть и другим у иных торговых марок. Отношение объёма воздуха (газа) в баке Wг0 при давлении p0 к общему объёму W обозначим как kб = Wг0/W. В рассматриваемом случае kб = 0,5.
Итак, при давлении воды в системе около 1,5 атм (или несколько ином случае, если в гидроаккумулятор накачано не равное 1,5 атм давление воздуха) вода будет занимать 50% объёма (либо несколько другое, что зависит от производителя данной модели бака).
Если верхний уровень давления p2 в системе, при котором, как правило, автоматика отключает подающий насос, задан выше давления pг0 = pв0 = p0 (в нашем случае 1,5 атм), то, согласно (4), соотношение объёмов Wг0 и Wг2 будет:
p0Wг01,4 = p2Wг21,4. (6)
Верхнее давление p2 относится, разумеется, и к воде, и к воздуху. Объём газа в баке составит Wг2 = W — Wв2, тогда:

где Wв2 — объём воды в баке при верхнем уровне давления p2.
Как правило, объём Wв2 больше, чем Wв0. Разница объёмов Wв2 и Wв0 составит ΔW2 = Wв2 — Wв0. Условно назовём объём ΔW2 «верхним». Тогда из (7) получаем:
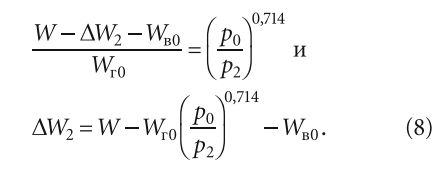
Нижний уровень давления p1 в системе, при котором, как правило, автоматика включает подающий насос, соотносится с давлением p0 как
p0Wг01,4 = p1Wг11,4. (9)
Точно так же, как верхний уровень, нижний уровень давления p1 относится и к воде, и к воздуху. Объём газа в баке составит Wг1 = W — Wв1, тогда:
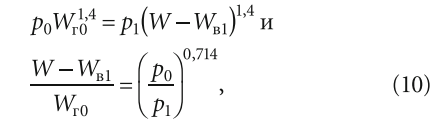
где Wв1 — объём воды в баке при нижнем уровне давления p1.
Предположим, что объём Wв1 меньше, чем Wв0 (хотя вполне возможна обратная ситуация). Разница объёмов Wв0 и Wв1 составит ΔW1 = Wв0 — Wв1. Условно назовём объём ΔW1 «нижним».
Тогда из (10) получаем:
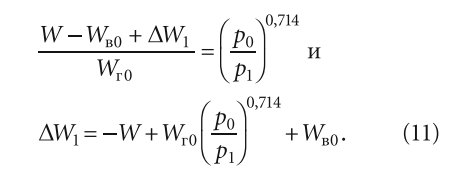
Разумеется, в зависимости от условий давление p1 может быть больше или меньше p0 — тогда и объём Wв1 будет соответственно больше или меньше Wв0. Аналогично можно сказать и о соотношении p2 и p0.
Объём ΔW, который можно назвать рабочим объёмом гидробака, складывается из «верхнего» и «нижнего» объёмов:
ΔW = ΔW2 + ΔW1, тогда:
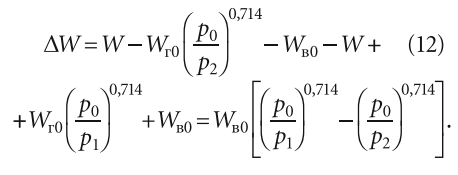
Отсюда
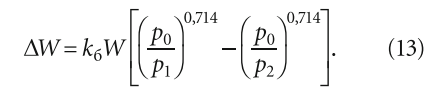
Таким образом, рабочий объём гидробака ΔW для данной модели и типоразмера прямо зависит от предварительно накаченного в бак давления p0, верхнего и нижнего уровней давления воды p2 и p1.
Как известно, подавляющее большинство насосов имеет ограниченное допустимое количество пусков в час. При расчётном расходе в системе водоснабжения Q (о котором речь пойдёт ниже) и допустимом количестве пусков насоса n требуемый запасной объём воды должен быть не менее nQ.
Приравняв nQ к ΔW, получим:
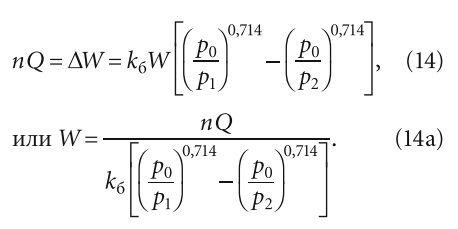
Уравнения (14) и (14а) связывают, таким образом, все основные показатели работы системы водоснабжения с бакомгидроаккумулятором:
- конструктивную особенность бака, которая выражается коэффициентом kб, учитывающим отношение объёма газа (воздуха) к полному объёму бака при равенстве изначально накаченного давления воздуха в баке p0 и давления воды в системе pг0;
- давление воздуха p0, изначально созданное в баке;
- верхний p2 и нижний p1 уровни давления воды в системе;
- рабочий объём бака ΔW; ? общий объём бака W;
- допустимое количество пусков насоса в час n;
- расчётный расход Q.
Выражения (14) и (14а) не учитывают сопротивление самой резиновой мембраны, которая обычно изготавливается из различных видов резины или EPDM.
Учёт данного параметра весьма затруднён вследствие значительного изменения модуля упругости резины или каучука при деформации. Оценить влияние мембраны возможно, по-видимому, с помощью поправочного коэффициента, определяемого путём натурных наблюдений за работой бака-гидроаккумулятора. При этом более или менее адекватно должен быть описан основной процесс работы гидроаккумулятора, который, по мнению автора, наиболее близок к адиабатическому газовому процессу.
Если провести оценку объёма бакагидроаккумулятора, исходя из выражений (2), (3), (14) и (14а), то возникает вопрос: в какой размерности следует подставлять значение расхода воды (вопроса относительно размерности давления не возникает, так как во всех указанных выражениях величины р делятся друг на друга)? Можно принять размерность для расхода воды в л/мин., как рекомендуется в пояснениях к формулам (2) и (3), рассмотрев получающиеся значения W на примере. Исходные данные для примерного расчёта приведены в табл. 1.

Примем изначально накаченное в бак давление воздуха равным р0 = 1,5 атм. Расчётный расход Qmax примем равным 5 м³/ч, что соответствует 1,4 л/с или 83,3 л/ мин., что является, в общем, небольшим расходом воды.
Значения давления рmax (p2) и pmin (p1) рассмотрим по трём вариантам:
1. рmax (p2) > p0, рmin (p1) < p0;
2. рmax (p2) > p0, рmin (p1) > p0;
3. рmax (p2) < p0, рmin (p1) < p0.
Результаты расчётов объёма бака-гидроаккумулятора, согласно (2), (3) и (14а) приведены в табл. 2.
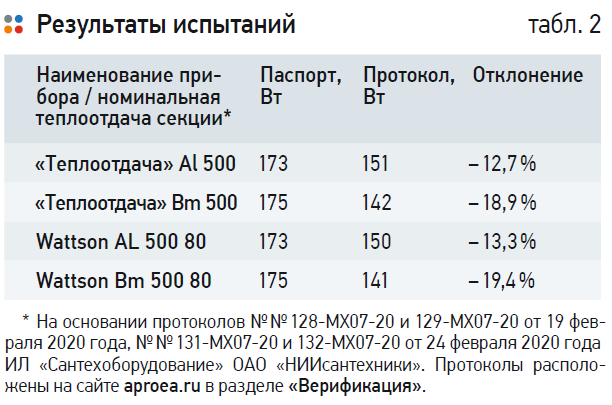
Столь большой разброс полученных значений объёма бака-гидроаккумулятора указывает, очевидно, на несовершенство расчётной модели. Это несовершенство, как можно предположить, связано с тем, какие расходы воды следует подставлять в расчётные формулы, а также с тем, какие технологические задачи вообще решаются с помощью бака-гидроаккумулятора. На первый взгляд ответ очевиден: бак-гидроаккумулятор предназначен для снижения количества пусков подающего насоса.
Однако при каких ситуациях необходимость снижения количества пусков насоса наиболее актуальна? Маловероятно, чтобы такая необходимость наблюдалась в период наибольшего водопотребления, когда подающие насосы работают почти постоянно и с максимальной частотой вращения двигателей, если речь идёт об агрегатах с частотными преобразователями. Наоборот, если водопотребление незначительное, бак-гидроаккумулятор становится весьма полезным, ведь самые малые объёмы воды, забранной из водопровода потребителем, могут резко снизить давление в трубопроводной системе, чем вызвать автоматическое включение подающего насоса. То же самое можно сказать и об утечках из труб, которые аналогичным образом снижают давление в системе и вызывают автоматическое включение насосных агрегатов. Следовательно, перед выбором типоразмера бака-гидроаккумулятора нужно определить, какой расчётный расход будет данный бак компенсировать, и каков располагаемый рабочий объём бака ΔW будет при заданных значениях p0, р2 и р1.
При этом типовой ряд баков-гидроаккумуляторов не так уж велик. Например, у известной торговой марки Zilmet представлены баки объёмом 24, 35, 50, 60, 80, 100, 200, 300, 500, 750, 1000, 1500, 2000, 3000, 4000 и 5000 л.
В нормативных документах [3–5] показаны расчёты максимального секундного, максимального, среднего, минимального часового расходов. Примечательно, что в более новом СП 30.13330 в отличие от СНиП 2.04.01–85* отсутствует расчёт максимального секундного расхода в зависимости от вероятности действия сантехнических приборов, что, разумеется, говорит не в пользу нормативных документов, принятых в постсоветское время.
Покажем возможный порядок расчё- та системы водоснабжения с баком-гидроаккумулятором на примере. Например, в посёлке проживает 300 человек, норма водопотребления при централизованном горячем водоснабжении составляет 250 л/ сут. на человека. Среднесуточный расход, следовательно, составляет 75 м³/сут. Коэффициент максимальной суточной неравномерности Кmax.сут, согласно [5], примем 1,2; максимальный суточный расход будет Qmax.сут = 90 м³/сут. Коэффициент минимальной часовой неравномерности Кч.min определяется как произведение коэффициента αmin, учитывающего степень благоустройства зданий (αmin = 1,3), и коэффициента βmin, учитывающего число жителей в населённом пункте (βmin = 0,03). Тогда средний часовой расход составит Qср.ч = 3,75 м³/сут., минимальный часовой расход — 0,146 м³/ч = 0,041 л/с.
Предположим, что для системы водоснабжения указанного посёлка предусмотрены верхний уровень давления р2 = 2,7 атм., нижний уровень давления р1 = 2,2 атм. Тогда, согласно выражению (14), при давлении р0 = 1,5 атм рабочий объём ΔW для бака объёмом 100 л составит 5,2 л, для бака 300 л — 15,5 л, для бака 500 л — 25,9 л и т. д. Следовательно, время сработки объёма ΔW при минимальном расходе 0,041 л/с (при переводе из 0,146 м³/ч) составит 127 с (2,1 мин.), 378 с (6,3 мин.) и 632 с (10,5 мин.).
Разумеется, представленный расчёт времени сработки рабочего объёма ΔW носит приблизительный характер, потому что, во-первых, в расчёте не учтено влияние сопротивления мембраны; во-вторых, расчётный расход (в данном случае минимальный часовой, выраженный в л/с) не может быть неизменным продолжительное время. Кроме того, следует признать, что у автора не было возможности проверить, насколько точно работает выражение (14) в реальных условиях. Возможно, проверка данной формулы будет темой какой-либо исследовательской работы. Постановка опыта представляется несложной: необходимо зафиксировать изменение (снижение) давления на манометре гидробака и отслеживать по показаниям водомера объём воды, выталкиваемой из бака-гидроаккумулятора в трубопроводную систему.
Нужно сказать, что такое устройство, как бак-гидроаккумулятор, необходимо при довольно простой автоматизации без частотного преобразователя для электродвигателя насоса с использованием реле давления, которое просто включает насос при падении давления до нижнего уровня (давление р1) и отключает при росте давления до верхнего уровня (давление р2). Понятно, что без гидроаккумулятора падение давления от р2 до р1 произойдёт намного быстрее, чем без бака.
При использовании частотного преобразователя явная необходимость применения бака-гидроаккумулятора неочевидна, так как есть возможность вовсе не выключать подающий насос. Для этого в шкафу управления с частотным преобразователем следует установить так называемый «спящий» режим, когда требуемое максимальное давление при отсутствии водопотребления поддерживается минимально возможной для данного типа насоса частотой тока электродвигателя, например, 17–20 Гц. Однако такое решение, несомненно, связано с повышенным расходом электроэнергии.
Возможен и другой вариант, позволяющий снизить количество пусков насоса при одновременном использовании частотного преобразователя и бакагидроаккумулятора: с помощью шкафа управления можно увеличить время задержки выключения подающего насоса при достижении требуемого максимального давления и частоты тока 50 Гц. В результате за данный промежуток времени давление поднимается несколько выше установленного верхнего уровня р2, что создаёт определённый запас давления и объёма воды, который будет срабатываться при последующем водопотреблении или за счёт утечек.
На практике встречаются примеры, когда несколько баков-гидроаккумуляторов присоединяют к одному трубопроводу, образуя своеобразную «батарею» из баков, ради увеличения общего регулирующего объёма.
По аналогии с баком-гидроаккумулятором применение таких вроде бы морально устаревших сооружений, как водонапорные башни, вполне может быть оправдано даже при использовании частотного преобразователя для погружного скважного насоса. Вполне возможно, что при использовании водонапорных башен экономия электроэнергии будет значительней, чем при использовании баков-гидроаккумуляторов. Но подтвердить данное предположение могут только практические исследования.

Выводы
1. Общей формулой для расчёта объёма баков-гидроаккумуляторов для небольших насосных станций второго подъёма и прямоточных схем водоснабжения может, по мнению автора, служить следующее выражение:
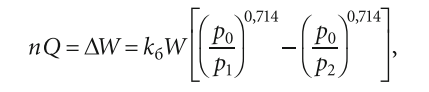
основанное на уравнении адиабатического газового процесса. Правомерность данного уравнения необходимо проверить практическими исследованиями.
2. Для адекватного подбора бака-гидроаккумулятора необходимо определиться с расчётным расходом, который будет компенсироваться рабочим объёмом бака ΔW. Рабочий объём бака ΔW определяется общим объёмом бака W, его конструктивными особенностями, давлением воздуха р0, изначально накаченным в бак, верхним р2 и нижним р1 уровнями давления воды в системе.
3. Баки-гидроаккумуляторы для насосных станций второго подъёма и прямоточных схем, как правило, требуются в небольших системах водоснабжения с подающими насосами без частотного регулирования.

























