
Рис. 1. Стенда для экспериментального определения гидравлических показателей канализационных труб из ПВХ
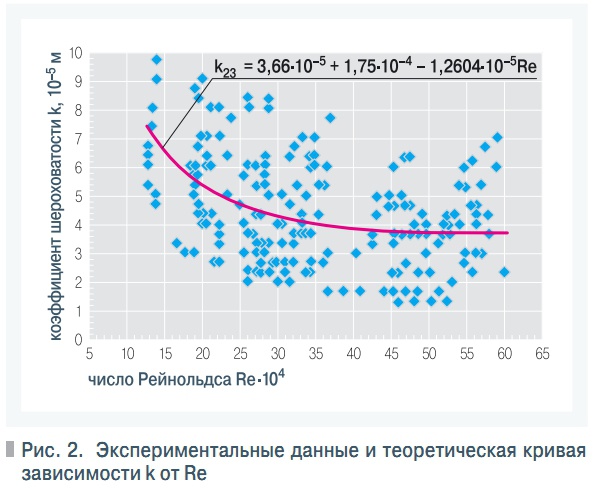
Рис. 2. Экспериментальные данные и теоретическая кривая зависимости k от Re

Рис. 3. Графическая экстраполяция экспериментальных осредненных зав-тей lg(100λ) = f(lgRe)
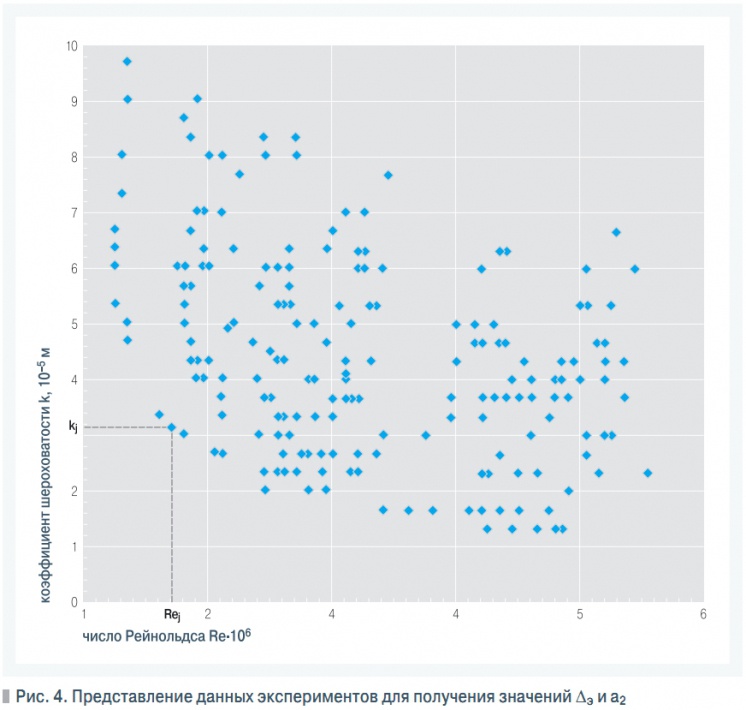
Рис. 4. Представление данных экспериментов для получения значений Δэ и a2
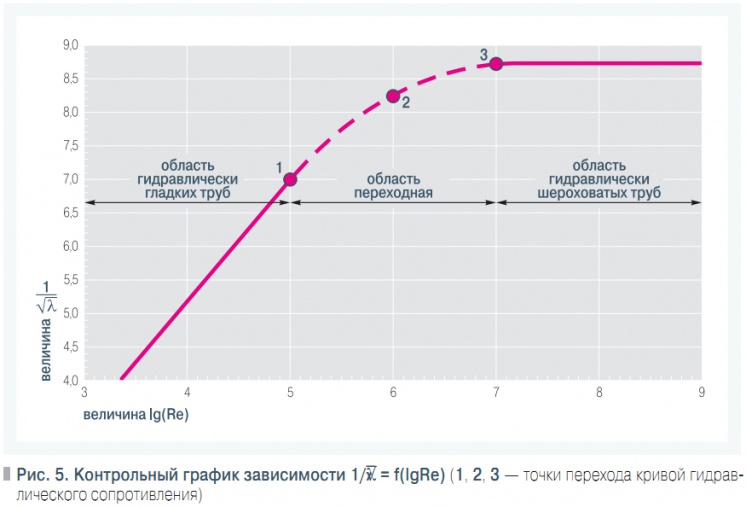
Рис. 5. Контрольный график зависимости 1/√λ = f(lgRe)

Рис. 6. Экспериментальные данные и теоретическая кривая λ = f(lgRe), построенная при Δэ = 0,00006 м и a2 = 20
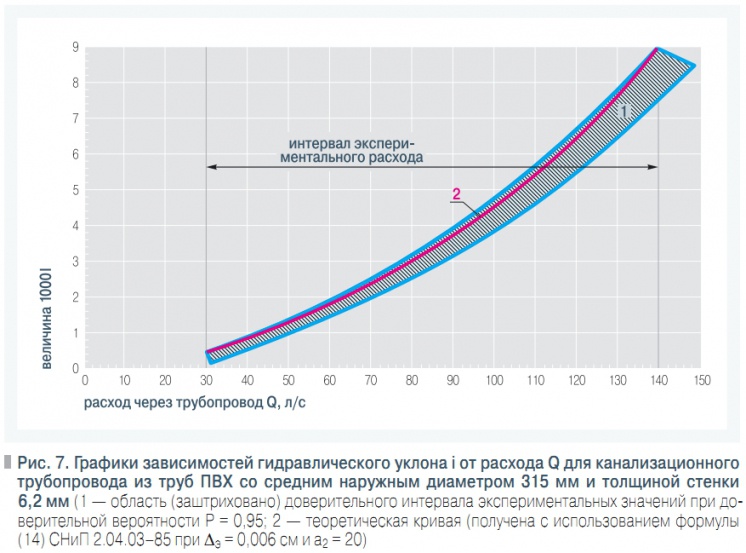
Рис. 7. Графики зависимостей гидравлического уклона i от расхода Q для канализационного трубопровода из труб ПВХ со средним наружным диаметром 315 мм и толщиной стенки 6,2 мм
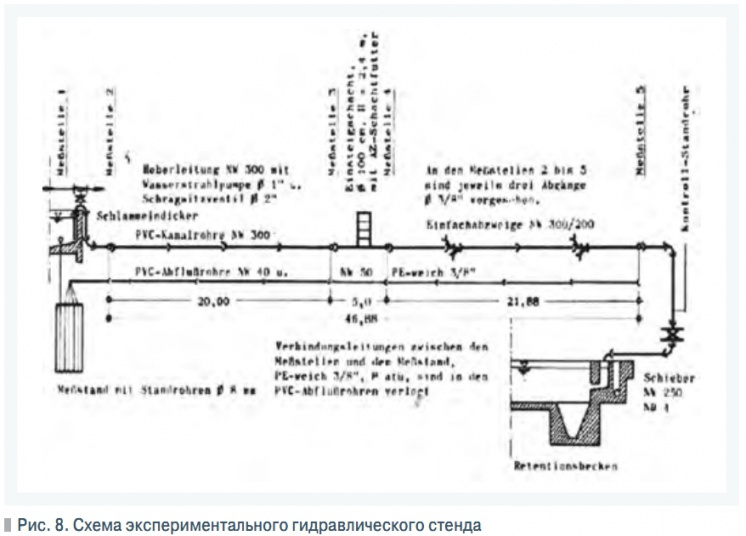
Рис. 8. Схема экспериментального гидравлического стенда
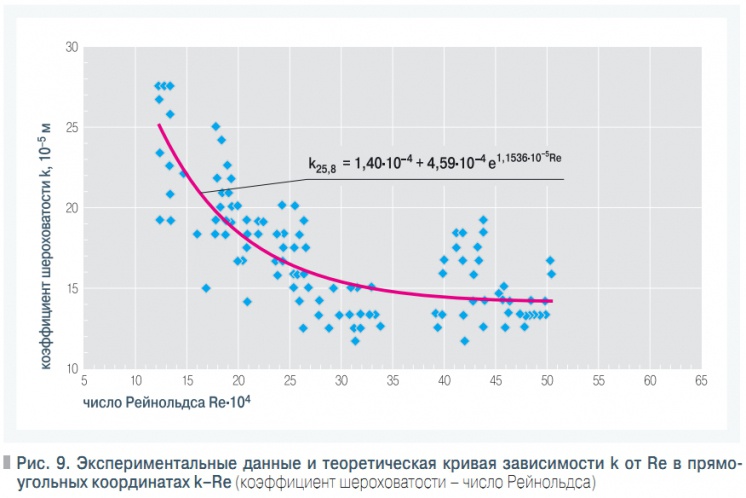
Рис. 9. Экспериментальные данные и теоретическая кривая зависимости k от Re в прямоугольных координатах k–Re
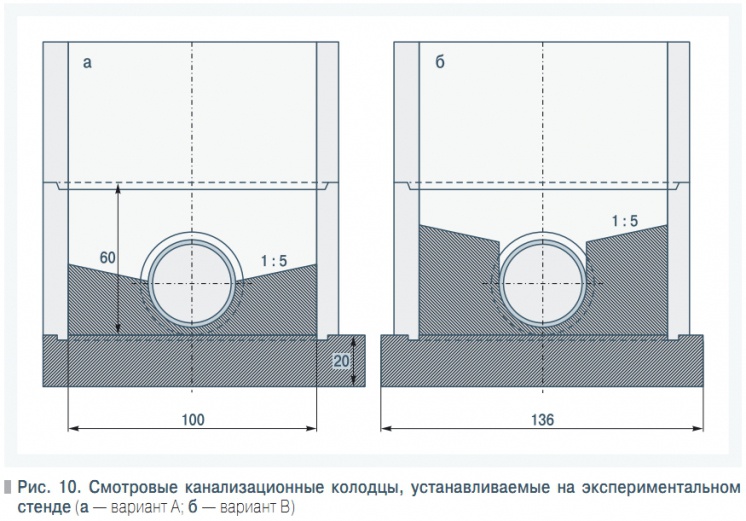
Рис. 10. Смотровые канализационные колодцы, устанавливаемые на экспериментальном стенде
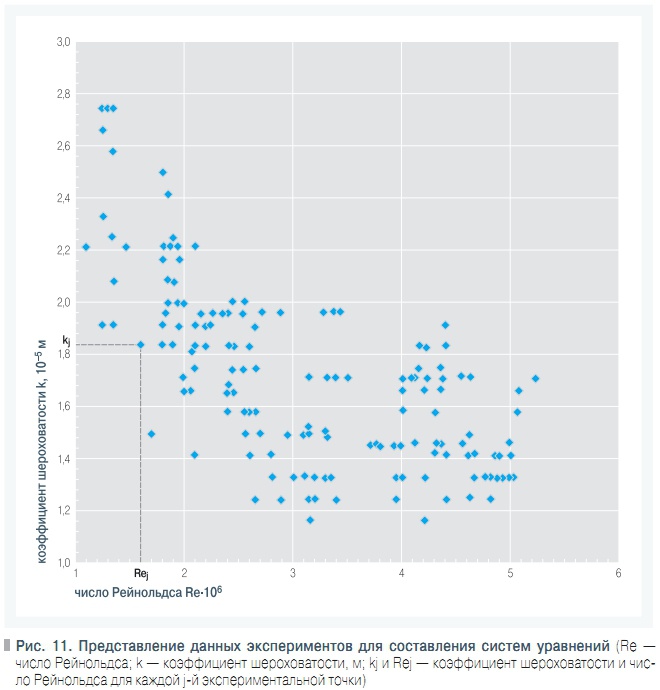
Рис. 11. Представление данных экспериментов для составления систем уравнений

Рис. 12. Графические зависимости
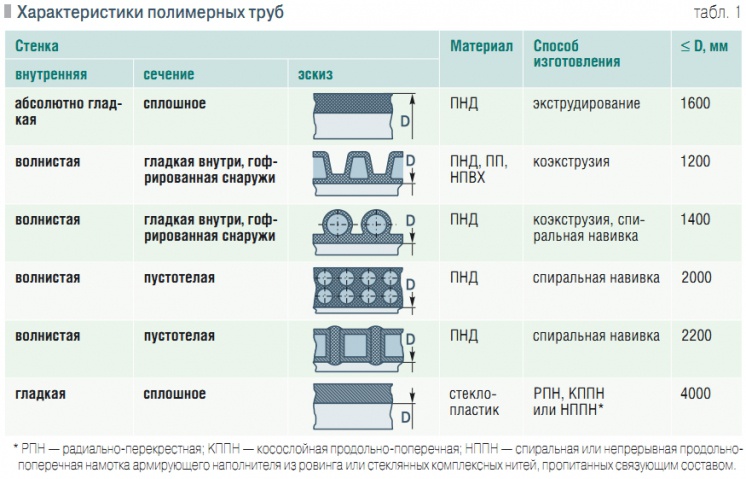
Табл. 1. Характеристики полимерных труб

Табл. 2. Значения D и а2
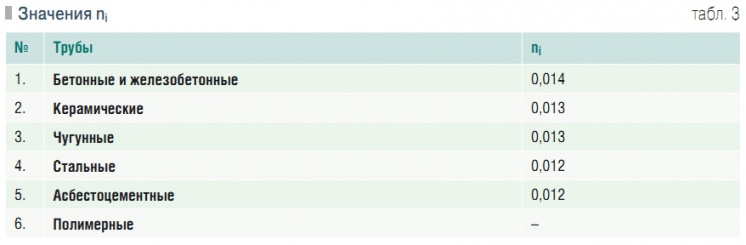
Табл. 3. Значения ni
Проектирование водоотводящих трубопроводов осуществляется, по-прежнему, с использованием положений СНиП 2.04.03–85 [1]. В них для гидравлических расчетов систем водоотведения приводятся соответствующие методики. Согласно одной из них, гидравлический уклон i водоотводящих трубопроводов

где g — ускорение силы тяжести, м/с2;λ — коэффициент сопротивления трению по длине, в СНиП 2.04.03–85 его следует определять по формуле (14) — именно для нее и будут определены эмпирические коэффициенты, учитывающей различную степень турбулентности потока
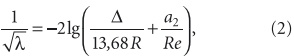
где D — эквивалентная шероховатость, см (табл. 2); R — гидравлический радиус, см; а2 — коэффициент, учитывающий характер шероховатости труб и каналов; Re — число Рейнольдса. Как следует из табл. 2, значения D и а2 для полимерных труб отсутствуют. В этой связи возникает вопрос — воз можно ли использовать эту методику для проведения гидравлических расчетов водоотводящих трубопроводов из таких труб?
Для ответа на этот вопрос в ГУП «НИИМосстрой» были обработаны экспериментальные данные [2], полученные доктором естественных наук Г. Суперспергом (H. Supersperg, г. Вена, Австрия), в соответствии с исследованиями проф. Н.Н. Федорова [3], собственно, по результатам которых и составлена формула (14), вынесенная в заглавие статьи.
Эксперименты доктор Г. Суперсперг проводил на стенде с самотечным трубопроводом из ПВХ-труб наружным диаметром Dт = 315 мм с толщиной стенки S = 6,2 мм (рис. 1).В процессе экспериментов фиксировались потери напора h (которые переводились в гидравлический уклон i и расход стоков Q (варьировался от 30 до 140 л/с) при полном наполнении труб. Результаты экспериментов представлялись графически зависимостью k = f(Re).Для получения значений k (коэффициент шероховатости) обработка экспериментальных данных осуществлялась с использованием зависимостей
Q = VF, (3)
где V — скорость движения стоков, м/с; F — площадь живого сечения трубы, м2.
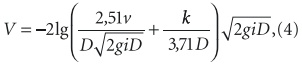
где v — коэффициент кинематической вязкости стоков, м2/с, в экспериментах его значения составляли 1,07⋅10–6 м2/с; D — внутренний диаметр трубопровода, м.Нами для получения значений Δэ и a2 использовались данные, отражающие течение стоков на участке «b–c» и представленные в статье доктора Г. Суперсперга в следующем виде (рис. 2).Для получения значений коэффициентов Δэ и a2 экспериментальные данные представлялись (рис. 3) в виде универсальной зависимости коэффициента гидравлического сопротивления λ от числа Рейнольдса Re [4] (Re = VD/v)
lg(100λ) = f(lgRe). (5)
Значения λj определены нами по формуле Прандтля-Кольбрука, которая на протяжении многих десятилетий является основой, для проведения практически всех гидравлических расчетов как самотечных, так и напорных трубопроводов, выполняемых проектными организациями большинства стран Европы, и именно она положена в основу формулы (4)

Значения kj и Rej брались для каждой jй точки (рис. 4). Обозначения: Re — число Рейнольдса; k — коэффициент шероховатости, м; kj и Rej — коэффициент шероховатости и число Рейнольдса для каждой jй экспериментальной точки. Предполагая, что экспериментальные точки лежат в переходной области сопротивления [4], была произведена графическая экстраполяция проходящей через них кривой (см. рис. 3) в область сопротивления гидравлически гладких труб и в область сопротивления гидравлически шероховатых труб [5].
После преобразования формул для коэффициента гидравлического сопротивления λ в области сопротивления гидравлически гладких труб и в области сопротивления гидравлически шероховатых труб относительно Δэ и a2 были получены выражения для них в явном виде

Подставив в выражения (7) и (8) соответствующие значения Re и λ, взятые с графика рис. 3 (для сопротивления гидравлически гладких труб λг = 0,0185 при Reг = 100 000 — точка 1 на кривой; для сопротивления гидравлически шероховатых труб λш = 0,0139 при Reш = 1 000 000 — точка 2 на кривой), а также Δт и S для труб, применяемых в эксперименте, 0,315 и 0,0062 м, соответственно, получили Δэ = 0,00006 м и a2 = 20. Эти значения несколько отличаются от известных величин. Для контроля, поэтому, строили графическую зависимость
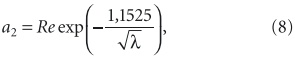
которая при полученных значениях Δэ = 0,00006 м и a2 = 20 имеет вид (рис. 5).Как следует из этого графика, начальная граница области гидравлически гладких труб нами выбрана правильно, она наступает при Re ≈ 100 000 (точка 1), а начальная граница области гидравлически шероховатых труб нами немного занижена, она наступает при Re ≈ 10 000 000 (точка 3), а не при Re ≈ 1 000 000 (точка 2), как принято.
Однако при полученных величинах Δэ = 0,00006 м и a2 = 20 коэффициент гидравлического сопротивления λ принимает значения, которые не превосходят ни одного экспериментального показателя — на кривую зависимости ложатся только шесть экспериментальных значений, отмеченных на рис. 6 крестиками. Это убеждает в том, что значения Δэ и a2 нами определены с достаточной надежностью.
Полученные значения Δэ = 0,00006 м и a2 = 20 позволили построить кривую зависимости гидравлического уклона i от расхода Q (рис. 7). Как видно из рисунка, эта кривая проходит вблизи доверительной границы меньших значений доверительного интервала при доверительной вероятности Р = 0,95, вычисленного нами для используемых выше экспериментальных значений.
Это убеждает в том, что такой подход к определению эмпирических коэффициентов Δэ и a2 имеет экономичное решение (за счет использования данных других исследователей, в данном случае зарубежного ученого — доктора Г. Суперсперга) и обеспечивает высокую надежность инженерных расчетов (за счет правильного использования методики обработки, в данном случае отечественного ученого — проф. Н.Н. Федорова).Согласно другой методики СНиП 2.04.03–85, гидравлический расчет водоотводящих трубопроводов надлежит производить с использованием следующей формулы
V = C√⎯⎯Ri, (10)
где С — коэффициент, зависящий от гидравлического радиуса и шероховатости смоченной поверхности канала или трубопровода и определяемый по формуле (в СНиП 2.04.03–85 — это формула (12), для нее и будет определяться эмпирический коэффициент):
C = Ry/ni, здесь (11)
y = 2,5√⎯⎯ni – 0,13 – 0,75R(√⎯⎯ni – 0,1), (12)
R — гидравлический радиус, м; i — гидравлический уклон; ni — коэффициент шероховатости, принимаемый для самотечных коллекторов круглого сечения 0,014, для напорных трубопроводов — 0,013.В работе [7] приводятся значения ni для труб из различных материалов (табл. 3). К сожалению, в табл. 3 отсутствуют значения ni для полимерных труб. Формула (12) СНиП 2.04.03–85 является математической моделью гидравлического сопротивления в шероховатой области.
Анализ литературы по вопросам гидравлики трубопроводов из полимерных труб показал, что для их расчета за рубежом широко используются формулы, характеризующие гидравлические сопротивления шероховатых труб (формулы Хазен-Вильямса, Маннинга, Стриклера и др.).С учетом этого в ГУП «НИИМосстрой» были обработаны опытные данные, полученные [2] на гидравлическом стенде (рис. 8).Обрабатывались данные, приведенные в первоисточнике для участка 2–5(рис. 9) с колодцем по варианту B (рис. 10), характеризуемым большим гидравлическим сопротивлением.
Для каждой экспериментальной точки с координатами kj и Rej (рис. 11), после соответствующего преобразования системы координат (из k → Re в 1000I → Q с использованием формулы Прандтля-Кольбрука для коэффициента гидравлического сопротивления λ, уравнения Дарси-Вейсбаха для гидравлического уклона I и выражения неразрывности струи для расхода Q была составлена система уравнений:
2,5√⎯⎯ni – yi = 0,13, (13)
lgni – Ayi = B – lgQi + 0,5lgIi, (14)
где ni — коэффициент шероховатости по акад. Н.Н. Павловскому (для полимерных труб неизвестен); yi — показатель степени, зависящий только от коэффициента шероховатости, так как R (гидравлический радиус) < 1 м (также неизвестен); А, В — постоянные, учитывающие диаметр труб; Qi — расход стоков, м3/с; Ii — гидравлический уклон. Решение составленных систем уравнений позволило принять в качестве расчетных значений верхнюю доверительную границу доверительного интервала для экспериментальных данных при доверительной вероятности
P = 0,95 → у = 0,125 и n = 0,0104.
Дальнейшие преобразования дали возможность получить степенные формулы для расхода стоков, аналогичные, например, формулам Хазен-Вильямса, которые широко используются в США и Японии для гидравлических расчетов трубопроводов, в том числе и из полимерных труб :
Q = 31,7D0,625I0,5, (15)
для скорости потока жидкости:
V = 40,4D0,625I0,5. (16)
Формула (15) с высокой степенью точности аппроксимирует верхнюю доверительную границу доверительного интервала, построенного для экспериментальных данных (рис. 12) при доверительной вероятности Р = 0,95 (коэффициент вариации между координатами точек, взятых с доверительной границы, и теоретической кривой, не превышает 3 %).
Таким образом, установлено, что для гидравлических расчетов водоотводящих трубопроводов из полимеров вполне допустимо использовать формулу (12)СНиП 2.04.03–85. И на данном этапе исследованности вопроса значения коэффициентов шероховатости в формуле (12) следует принимать — для полимерных труб ni = 0,01.Далее, заменив внутренний диаметр труб D на гидравлический радиус R, получили
V = 96,2R0,625I0,5. (17)
Сравнивая эту формулу, например, с формулой Хазен-Вильямса
V = Ch–wR0,63I0,54, (18)
замечаем их близкое совпадение. В формулу (18) при проведении гидравлических расчетов подставляется (5) значение коэффициента Ch–w, например, для полиэтиленовых труб диаметром 1000 мм равное 150.Из рассмотренного можно сделать вывод о том, что полученное в результате обработки экспериментальных значение коэффициента шероховатости ni несколько завышено.
Тем не менее, принятую по результатам обработки экспериментов на трубах диаметром 300 мм величину коэффициента шероховатости (ni = 0,01) можно использовать для гидравлического расчета (по формуле (12) СНиП 2.04.03–85) водоотводящих трубопроводов из полимерных труб всех диаметров.


























