Движение потоков в сооружениях водоочистки с аэрацией (например, аэротенк, аэрофильтр, аэрируемая песколовка) создают технологическую особенность. Основным процессом, в физическом понимании аэрации, является движение пузырьков воздуха снизу вверх. Рассмотрим всплывание пузырька воздуха в жидкости, находящейся в состоянии покоя.
Предположим, что пузырёк воздуха в жидкости имеет форму шара [1].
На всплывающий пузырёк действуют три силы: сила тяжести Fт, архимедова сила Fа и сила сопротивления Fc (рис. 1). В проекции на вертикальную ось OY подъёмная сила Fп равна:

Силы выражаются в ньютонах (Н).
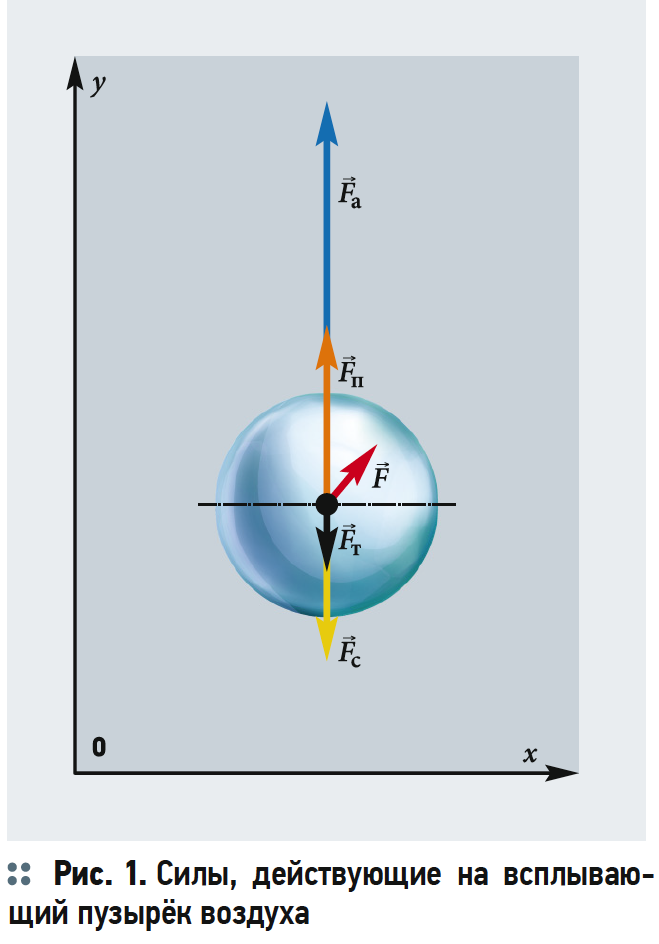
Рассмотрим действие сил при равномерном движении пузырька в воде.
Сила Архимеда (выталкивающая сила) приводит пузырёк в движение вверх, при этом диаметр пузырька увеличивается, достигая своего максимума на поверхности воды.
Сила Стокса (сила трения) при движении пузырька действует в направлении, противоположном силе Архимеда, и направлена сверху вниз.
Сила тяжести действует в условиях ускорения свободного падения и направлена сверху вниз.
Сила Стокса возникает в результате взаимодействия жидкости с пузырьком и равна силе трения, на преодоление которой затрачивается работа.
Разность энергий двух состояний пузырька до начала совершения работы и после — это работа как избыточная свободная энергия. С точки зрения гидростатики дополнительная потенциальная энергия равносильна динамическому напору.
При условии сжимаемости воздуха и при движении пузырька вверх наружное давление на стенки пузырька будет меняться с высотой, а диаметр пузырька будет увеличиваться. Расширение воздуха в пузырьке может происходить либо изотермически, либо адиабатически. Поскольку размер пузырька определяют условия гидростатики и силы Стокса, то принимаем расширение воздуха в пузырьке как изотермическое, поэтому размеры пузырька должны быть достаточно малыми.
Запишем условие для изотермического процесса при вертикальном всплытии пузырька воздуха:
pV = const, (2)
где p — давление жидкости, Па; V — объём жидкости, м³.
Если p0 — атмосферное давление [Па], то давление на глубине h [м] в жидкости плотностью ρ [кг/м³] будет равно (p0 + ρgh), где g — ускорение свободного падения, g = 9,81 м/с2; ρ — плотность жидкости, кг/м³; h — глубина, м.
Согласно закону изотермического расширения пузырька (2) на глубине слоя жидкости найдём радиус пузырька:

где r0 — радиус пузырька на поверхности воды, мм.
Пузырёк движется со скоростью v в жидкости, характеризуемой динамической вязкостью [Па·с]. Движение сферического пузырька в жидкости, которая рассматривается как непрерывная среда, и размеры которого (пузырька) значительно превышают размеры молекул среды, описывается уравнением Стокса для вязкого сопротивления:

где Fc — сила Стокса, Па; м — динамическая вязкость, Па·с или Н·с/м²; v — скорость всплытия пузырька, м/с.
Сила Архимеда Fа (подъёмная сила для пузырька) определяется из выражения

и она равна силе Стокса.
Сила тяжести равна:

где m — масса пузырька, кг.
Сила тяжести зависит от геометрических размеров пузырька. Эта сила крайне мала в сравнении с силами, действующими на пузырёк воздуха в воде, следовательно, значением силы тяжести можно пренебречь.
Скорость всплывания пузырька находится по уравнению:

От шарообразной формы переходим к изменению форм пузырька [2, 3].
Пузырёк находится в движении во время подъёма до поверхности воды. При этом пузырёк воздуха принимает шарообразную форму за счёт действия сил поверхностного натяжения.
Кроме того, изменение давлений сред (внутренней и внешней) пузырька приводит к деформации его поверхности, что способствует колебанию пузырька.
Применительно к единичному всплывающему пузырьку, на границе раздела фаз возникает разность давлений Δр, описываемая уравнением:
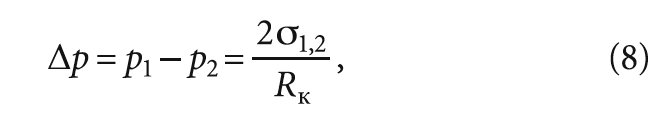
где р1 и р2 — давления двух фаз на глубине, Па; σ1,2 — поверхностное натяжение на границе двух фаз, Н/м; Rк — радиус кривизны поверхности рассматриваемого пузырька, м.
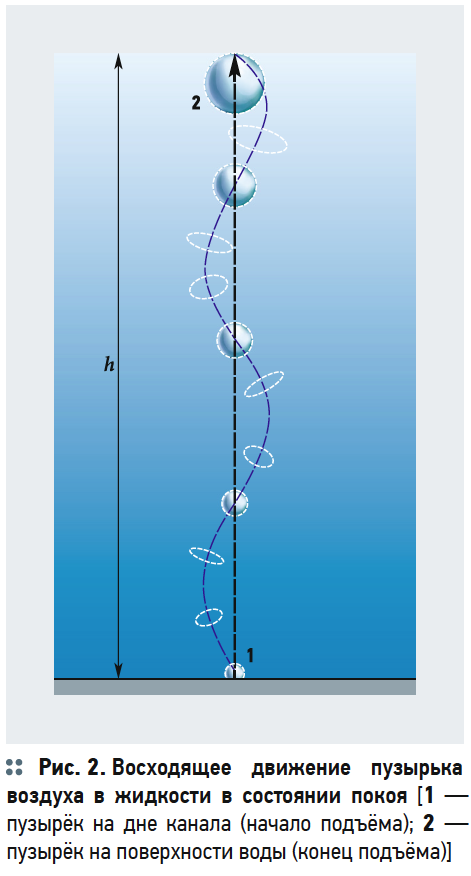
В результате увеличения объёма и изменения формы пузырька возникают его колебательные движения. Траектория всплытия пузырька принимается смещающейся относительно вертикали и носит волновой характер (рис. 2).
Теперь известны все величины, определяющие силу Стокса, что позволяет вычислить работу, совершаемую всплывающим пузырьком.
Вертикальное направление всплывания пузырька выберем за ось Oy.
Увеличение размеров и изменение формы пузырька передаётся окружающей пузырёк жидкости. Тем самым возникает суммарная работа dA и приращение свободной энергии согласно силам, действующим на пузырёк (рис. 1).
Поэтому приращение свободной энергии du в пересчёте на один пузырёк определится равенством:

где du и dA выражаются в джоулях (Дж).
Используя в формуле (9) выражения для силы Стокса (4), радиуса пузырька (3) и скорости всплытия пузырька (7), получаем следующий результат:
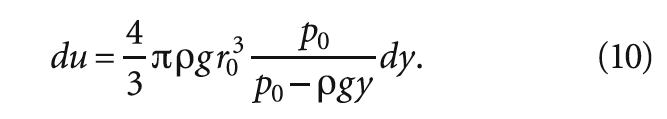
Для расчёта свободной энергии пузырьков введём функцию распределения f (r), которая представляет собой плотность вероятности обнаружения размера пузырька в единичном объёме между пузырьками с радиусами r и (r + dr).
Количество пузырьков с такими размерами в объёме dV будет равно f (r)drdV, поэтому их вклад в свободную энергию запишется как:
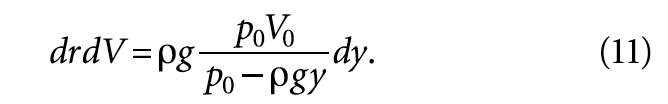
Помня, что V0 = 4/3(πr03), и интегрируя по всем возможным размерам пузырьков, получаем:
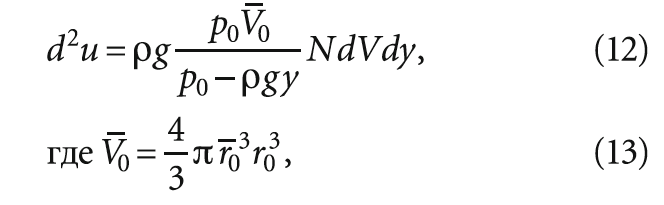
здесь r_ 03 — среднее значение куба радиуса пузырька на уровне поверхности жидкости, мм³; количество пузырьков в единице объёма жидкости, шт.
Термодинамическая связь параметров системы определяет давление р в системе как производную свободной энергии по объёму. Избыточное давления жидкости тогда составит:
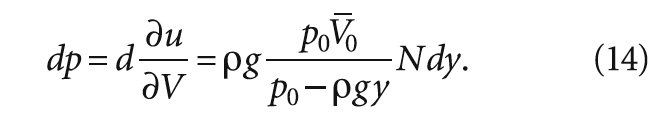
Рассмотрим всплытие пузырька воздуха в потоке жидкости при ламинарном режиме течения.
На рис. 3 представлена схема воздействие потока жидкости на вертикальное всплывание пузырька воздуха. Под воздействием распределения скоростей потока v = f(h) происходит смещение пузырька от вертикальной оси Oy. Согласно основным законам гидродинамики распределение скоростей зависит от кинетической энергии потока [3, 4]. По сечению потока происходит распределение скоростей, которые зависят от сопротивления между слоями жидкости при движении.
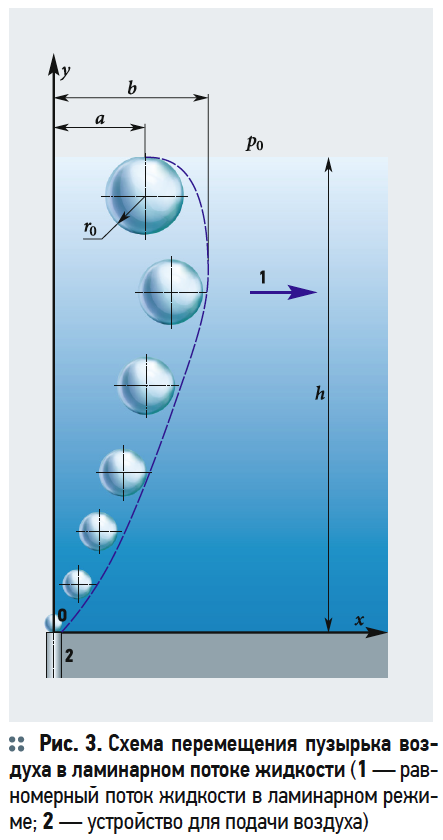
Нижние слои потока имеют сопротивление движению за счёт шероховатости дна, а движение верхнего слоя замедляется на границе раздела фаз «вода-воздух».
Обозначим через a [мм] расстояние от оси Oy до всплывшего пузырька на поверхности жидкости, а через b [мм] расстояние от оси Oy до всплывающего пузырька, максимально сместившегося по направлению движения жидкости.
Разница между a и b всплывающего пузырька зависит от скорости потока. Тогда выражение (14) запишется как
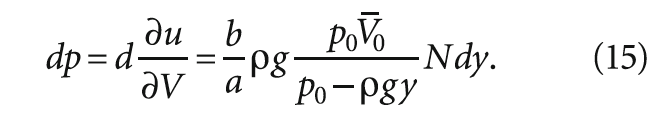
Полученная математическая зависимость позволяет более точно осуществить численные эксперименты на определённом этапе проектирования аэрационных сооружений систем водоочистки.
Эти действия направлены на нормализацию неустойчивости работы аэрационных сооружений и на определение оптимальных условий технологического процесса.
Выводы
1. Произведён анализ воздействия физических факторов на движение пузырька воздуха в воде, основанный на изотермическом процессе.
2. Получено уравнение, в котором приводится термодинамическая связь в определении давления в системе, как производная свободной энергии в потоке воды с учётом гидродинамических отклонений.
3. Использование полученного выражения позволяет повысить эффективность процесса водоочистки с применением аэрации.
























