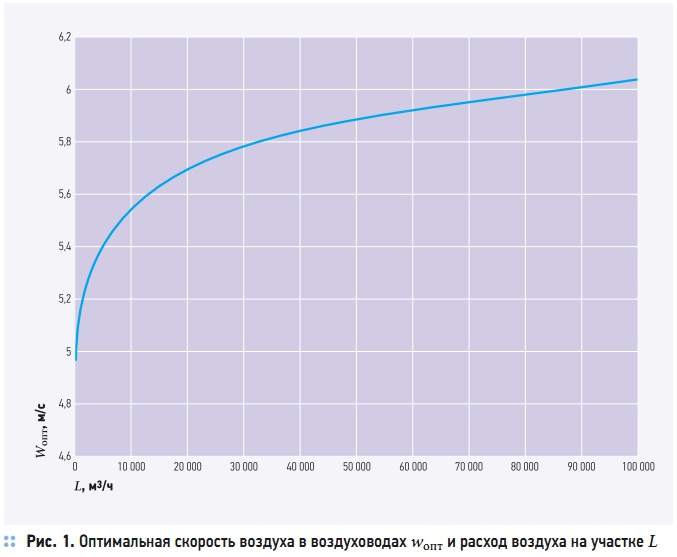
Рис. 1. Оптимальная скорость воздуха в воздуховодах wопт и расход воздуха на участке L
Как известно, основная идея технико-экономической оптимизации какого-либо инженерного решения и, в частности, энергосберегающих мероприятий при использовании метода совокупных дисконтированных затрат (СДЗ) [1] заключается в нахождении значения некоторого параметра, характеризующего степень реализации данного мероприятия, при котором величина СДЗ принимает минимальное значение для заданного расчетного срока Т.
В качестве параметра может быть, например, сопротивление теплопередаче ограждения, диаметр трубопровода или воздуховода, скорость теплоносителя, габариты вентиляционной установки, температурная эффективность теплоутилизатора и т.д. Оптимизация возможна, если при одном и том же изменении параметра капитальные затраты К увеличиваются, а эксплуатационные Э — уменьшаются или наоборот, т.е. меняются в разных направлениях.
Например, при повышении теплозащиты ограждающих конструкций, с одной стороны, снижаются расходы Э на тепловую энергию за счет уменьшения трансмиссионных теплопотерь, а с другой — возрастают затраты К на теплоизоляционный материал. Аналогично, при уменьшении диаметров трубопроводов или воздуховодов сокращается их стоимость К из-за уменьшения массы металла, но увеличиваются затраты на электроэнергию Э для привода насосов или вентиляторов вследствие возрастания потерь давления при движении теплоносителя.
Таким образом, технико-экономическая оптимизация представляет собой обобщение примеров, когда сравниваются только два варианта, для которых выполняется соотношение К1 > К2, но Э1 < Э2, потому что теперь речь идет о бесконечном множестве непрерывно переходящих друг в друга сочетаний параметров, среди которых и нужно выбрать наилучший в смысле минимальной величины СДЗ.
Рассмотрим задачу технико-экономической оптимизации диаметров воздуховодов систем механической вентиляции и кондиционирования воздуха (В и КВ). В работе [2] для удельных потерь давления на трение в стальных воздуховодах было получено выражение:
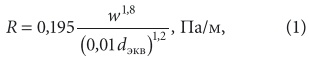
где w — скорость воды в трубопроводе, м/с; dэкв — эквивалентный диаметр воздуховода, мм. Удельная мощность, необходимая для перемещения воздуха через один погонный метр воздуховода, может быть определена по следующей формуле [3]:
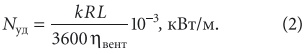
где L — объемный расход воздуха на рассматриваемом участке воздуховода, м3/ч; k — коэффициент учета потерь на местных сопротивлениях, который при их доле в общей сумме, равной примерно 0,75, составит 1/(1 – 0,75) = 4; ηвент — коэффициент полезного действия вентилятора в приточной или вытяжной установке. Для обычно используемых радиальных вентиляторов низкого и среднего давления одностороннего и двустороннего всасывания среднее значение ηвент можно принимать в размере около 0,7.
Если теперь выразить скорость воздуха через его расход и диаметр воздуховода и подставить в соотношение для Nуд, получаем формулу для эксплуатационных затрат на электроэнергию для привода вентилятора, отнесенных к одному погонному метру:
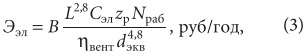
где В = 3,92 — коэффициент, получающийся из постоянных величин, входящих в выражения для Ээл, R и Nуд; Сэл — тариф за электрическую энергию, руб/(кВт⋅ч). В отличие, например, от системы отопления, системы вентиляции и кондиционирования воздуха, как правило, действуют не круглосуточно, но чаще всего круглогодично или, по крайней мере, за исключением нерабочих дней, поэтому при расчете энергозатрат на привод продолжительность рабочего времени zр, часов в сутки, и число рабочих дней за год Nр в формуле (3) должны приниматься, исходя из действительного режима работы систем. Капитальные затраты на воздуховоды с комплектующими будут пропорциональны поверхности воздуховода, а значит, тоже будут зависеть от диаметра.
В данном случае, в отличие от систем отопления, эта зависимость в первом приближении будет всетаки линейной, поскольку удельная поверхность одного погонного метра связана с dэкв для круглых воздуховодов очевидным соотношением Fуд = πd × 10–3 (в данном случае dэкв = d — фактический внутренний диаметр). Отсюда для капитальных затрат получаем:
Квв = Cввπd × 10–3, руб. (4)
где Свв — стоимость воздуховодов с комплектующими в расчете на 1 м2 поверхности воздуховода с учетом повышающего коэффициента на монтаж и наладку, равного примерно 1,5–1,6.В работе [4] предлагается следующая формула для СДЗ:
СДЗ = К(1 + 0,01p)T + Э[(1 + 0,01p)T – 1]100p–1, (5)
где p — норма дисконта, %. Она учитывает упущенную выгоду от того, что средства в размере К вложены в энергосбережение вместо размещения под проценты в банке. В расчетах ее можно принимать на уровне не ниже ставки рефинансирования Центрального Банка России. По состоянию на середину 2010 г. она равна 8,25 % годовых. Величина р связана с текущей величиной этой ставки, а также с коммерческими рисками капиталовложений.
В [1] предлагается использовать на ближайшую перспективу значение р = 10 %.Подставляем соотношения для Квв и Ээл вместо К и Э в (5), вычисляем производную d(СДЗ)/d(d) и приравниваем ее нулю, откуда после некоторых преобразований для оптимального значения d [мм] находим:
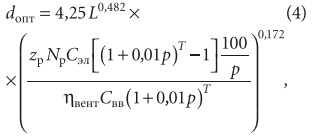
Принимая:Nр = 365 сут., zр = 12 ч,Свв = 400 × 1,5 = 600 руб/м2по среднерыночной цене 2010 г. для спиральных воздуховодов,hвент = 0,7, Сэл = 3,01 руб/(кВт⋅ч)по данным ОАО «Мосэнергосбыт» для нежилых потребителей на 2010 г. и р = 10 % годовых, как в предыдущих примерах, для Т = 5 лет — dопт = 9,67L0,482.Анализ формулы (6) показывает, что стоимость энергетических ресурсов и суровость климатических условий оказывают повышающее воздействие на оптимальный диаметр, а стоимость материала — понижающее.
Однако показатель степени при расходе воздуха весьма близок к 0,5, что позволяет предположить очень слабую зависимость оптимальной скорости воздуха от воздухо-производительности, что и будет показано ниже. Для данной задачи к повышению dопт приводит еще и увеличение значений Nр и zр, потому что это тоже вызывает рост фактического потребления электроэнергии. Выражая оптимальную скорость воздуха через его расход и оптимальный диаметр воздуховода, получаем следующую зависимость [м/с]:
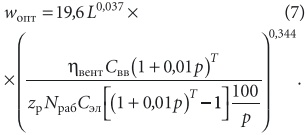
или при Т = 5 лет — wопт = 3,94L0,037 (для Москвы), что в условиях рассматриваемого примера дает величину около 5,4 м/с, если принять L = 5000 м3/ч. Для расхода воздуха вентиляции, равного 15 000 м3/ч, оптимальная скорость будет несколько выше и составит 5,63 м/с. В целом, это соответствует обычному уровню скоростей в воздуховодах, рекомендуемому для гражданских зданий [3].
Заметим, однако, что при использовании других значений параметров, входящих в формулу (7), получаемые данные будут варьироваться в достаточно узких пределах, поскольку показатели степени при переменных и их комплексах невелики, так что порядок результата сохраняется. На рис. 1 представлена зависимость wопт от L при Т = 5 лет. Видно, что при росте расхода величина wопт действительно приближается к величине 6 м/с [3], так что ее можно рассматривать как некоторую предельную при максимальном L.
Следовательно, в среднем можно принимать wопт порядка 5,5–6 м/с, а при малых расходах — около 5 м/с, и вычислять оптимальный диаметр по формуле:dопт = (7,8–8,4)√⎯L. Таким образом, мы получили методику технико-экономической оптимизации диаметров воздуховодов систем механической вентиляции и кондиционирования воздуха, учитывающую текущие значения цен и тарифов на материалы и энергоносители, а также уровень инфляции и рисков капиталовложений. Методика достаточно проста и пригодна для использования в инженерной практике и учебном процессе.

























