Обобщенная матмодель стационарного нелинейного переноса

Введение

Процессы тепло и массопереноса, фильтрации парогазовых смесей и жидкостей через капилляры твердых ОК весьма сложны и тесно взаимосвязаны. Кроме того, в зависимости от периода года эти процессы сопровождаются такими физическими явлениями, как испарительное охлаждение или конденсационный нагрев. Осуществление же плотного наружного слоя ОК помещений возможно не во всех случаях, так как такое конструктивное решение может ухудшить влажностное состояние ограждения из-за трудностей воздухопроницаемости в ОК, а следовательно, и ее просушки в летний период года, см. работы [1–5].

Современные многослойные энергосберегающие ОК (под которыми в широком смысле могут подразумеваться также тепловые или инженерные сети, емкости и резервуары для подогрева, охлаждения или хранения каких-либо жидкостей или газов и т.п.) в основном состоят из капиллярно-пористых твердых материалов, которые находят все большее применение не только в строительстве, но и во многих других отраслях промышленности (высокотемпературные теплообменники; тепловые, электрические и инженерные сети; турбинные лопатки; ракетные сопла; обшивка скоростных летающих аппаратов; обмуровка теплои электрогенерирующих установок, системы ядерных реакторов с внутренним охлаждением и т.д.), где различные элементы оборудования подвержены достаточно высоким термическим напряжениям, возникающим в результате больших градиентов температуры ∇t [6–10].

Основная часть

Перенос тепловой энергии в ОК происходит через твердый скелет материала, жидкую и парообразную влагу, которые содержатся в капиллярно-пористых телах. Уравнение стационарного нелинейного переноса с учетом фильтрации (газа, парогазовой смеси, жидкости) и наличия внутренних объемных стоков (влаги) или ИТ при общепринятых допущениях [1–5] в одномерном случае применительно к каноническим формам в соответствующих системах координат в общем случае может быть записано в виде обыкновенного дифференциального неоднородного уравнения второго порядка [11–12]:

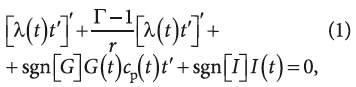
где t(r) — температура; r — текущая координата, r ∈ [0, h], здесь h — толщина многослойной ОК; λ — коэффициент теплопроводности ОК (возможно с учетом ее объемной пористости П); Γ — постоянная формы (Γ = 1, 2 и 3 — это неограниченные пластина, цилиндр или квадратный брусок, шар или куб, соответственно); c_p — изобарная теплоемкость паровоздушной смеси; G — плотность потока паровоздушной смеси, здесь «+» означает процесс эксфильтрации, а «—» — инфильтрации паровоздушной смеси; I(t) — мощность внутреннего ИТ (+) или стока (—); «`» (верхний штрих) — дифференцирование по r; sgn[⋅] — (сигнум) функция «знак».

Если I = const, то в рассматриваемой области термических сопротивлений действует непрерывно равномерно распределенный положительный или отрицательный ИТ. Если I (t) ≠ const, то в этой области действуют местные, сосредоточенные или распределенные положительные или отрицательные ИТ.

При обобщенном физическом описании процессов охлаждения ОК (возможно и испарительного) или нагрева (возможно и конденсационного) аналогично уравнению (1) могут быть составлены тепловые балансы как для области r ∈ [-∞, 0], так и для области r ∈ [h, +∞], которые приводят к новым дифференциальным уравнениям набегающего к ОК и отходящего от ОК потоков газа (или жидкости) с соответствующими для новых закрытых интервалов r граничными условиями. В этом случае к дифференциальному уравнению (1) добавляются в зависимости от условий задачи еще один или два дифференциальных уравнения второго порядка и соответственно два или четыре граничных условия. Таким образом, обобщенная ММ даже только для стационарного теплопереноса в ОК должна содержать в себе три дифференциальных уравнения второго порядка и шесть граничных условий для нахождения соответствующих констант интегрирования. В этом случае температурное поле t (r) в ОК выражается через температуры окружающего воздуха (газа, жидкости, теплоносителя или хладагента) по обе ее стороны. В более упрощенном варианте эти граничные дифференциальные уравнения для ОК заменяются краевыми условиями третьего рода с возможным учетом на границе поверхностей ОК поверхностных стоков или ИТ [6–9].

В свою очередь, уравнение (1) с граничными условиями третьего рода может быть заменено более простыми граничными условиями первого рода при условии ввода постоянных фиктивных (эквивалентных) пограничных слоев. Анализ конвективного теплообмена показывает, что в этом случае граничные условия третьего рода фактически отображаются в граничные условия первого рода. Тогда при интегрировании уравнения (1) и наличии в граничных условиях двух изотермических поверхностей вполне можно использовать преобразование Кирхгофа [7, 9], которое через новую вспомогательную переменную θ и средний коэффициент теплопроводности λ_c приводит дифференциальное уравнение (1) к формализации следующей краевой задачи:

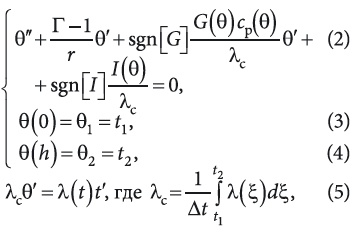
Δt = t₂ — t₁, t₂ > t₁, t₁ и t₂ — температуры противоположных поверхностей ОК. Направление потока тепла относительно r ≥ 0 определяется граничными условиями задачи.

Формализованную задачу, выражающуюся уравнениями (2)—(4) можно переписать в критериальном виде через критерии Пекле (Pe) и Померанцева (Po) и безразмерных масштабах температуры (T) и термического сопротивления (R), что особенно удобно, так как позволяет перевести многослойную ОК в однослойную. В этом случае, опуская промежуточные преобразования, задачу (2)—(4) можно записать в виде:

где T — безразмерная температура:

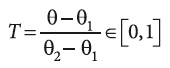
а R — величина безразмерного термического сопротивления:

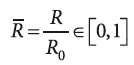
здесь R = r/λ — текущее термическое сопротивление; R₀ — общее термическое сопротивление (суммарное, приведенное, требуемое или многослойной стенки), которое выбирается в зависимости от принятых граничных условий. А данные параметр тогда Pe равен G(T)c_p(T)R₀ (в строительной теплофизике выражение Gc_pR₀ называют относительным коэффициентом фильтрационного теплообмена [3], характеризующим отношение тепловой емкости потока воздуха Gc_pR₀ к коэффициенту теплопередачи ограждения К = 1/R₀).

Если учесть объемную пористость ограждающей конструкции, то

в этой постановке задачи ΔT в критерии Померанцева можно опустить, так как максимальный перепад температур равен единице; «ʹ» (верхний штрих) — дифференцирование по R.

Если же известны пределы изменения Pe и Po, то знак сигнатуры в уравнении (6) в принципе можно опустить, если рассматривать эти критерии только в интервале [0, 1]. Тогда критерии Пекле и Померанцева запишутся в виде

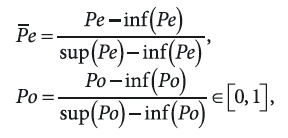
В этом случае все зависимые и независимые переменные и параметры поставленной краевой задачи безразмерны и лежат в четырехмерном нормированном единичном пространстве (T, R , Pe , Po ). Тогда система (6)—(8) перепишется в следующем виде:

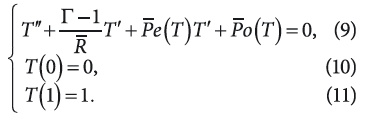
Таким образом, приведенные преобразования значительно упрощают математическую формализацию задачи, устраняют физические размерности и знаки, решают вопросы масштабного перехода. Единственно, несколько усложняется физическая интерпретация задачи, особенно когда в вышеуказанном пространстве строится графическое решение задачи, где фактически как бы «теряются» направленность потока (G) и знак ИТ (I) из-за отсутствия отрицательных значений параметров задачи на закрытом интервале [0, 1], но это усложнение легко устраняется при обратном переходе к первоначальным параметрам задачи.

Рассмотрим в качестве примеров несколько упрощенных частных случаев решения поставленной краевой задачи, часть из которых сводится к известным решениям, изложенным в работах [1–9].

I. При Γ = 1, λ(t), Pe = const, Po = const и искусственно опущенного знака сигнатуры (так как Pe и Po ∉ [0, 1]), краевую задачу (6)—(8) можно записать в форме:

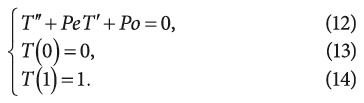
где при Pe < 0 происходит инфильтрация в ОК, при Pe > 0 — эксфильтрация, при Pe = 0 — фильтрация воздуха отсутствует; при Po < 0 действует отрицательный ИТ, при Po > 0 — положительный ИТ, при Po = 0 — ИТ отсутствует.

Аналитическое решение краевой задачи (12)—(14) получено в виде:

которое уже охватывает все комбинации вышеперечисленных частных случаев параметров переноса (Pe, Po) при заданных условиях однозначности.

Таким образом, в зависимости от знака и величины Pe или Po, имеем различные ММ, отражающие соответствующие им физические процессы (явления). При условии же ввода в уравнение (12) Pe и Po ∈ [0, 1] обобщенная физическая интерпретация поставленной задачи и полученное в этом масштабе решение несколько усложняется ввиду отсутствия в ММ и ее решении отрицательных значений Pe и Po . Кроме того, необходимо отметить, что частное решение (15), несмотря на видимую простоту, получено все же при функциональной зависимости коэффициента теплопроводности от температуры λ[t(r)].

Поэтому, если λ(t) ≠ const, то для получения профиля t(r) необходимо полученное решение T(R ) первоначально перевести в θ(r), а далее обратным переходом через преобразование Кирхгофа (5) найти уже поле температур t (r) в исходных обозначениях поставленной задачи. Алгоритм такого перехода рассмотрен на нижеследующем примере.

II. При Γ = 2, λ(t) = λ₀(1 + β_t), где λ₀ — известный коэффициент при контрольной температуре t₀, β — температурный коэффициент теплопроводности, Pe = 0 и Po = 0, получим промежуточное известное решение задачи (2)—(4) в следующем виде:

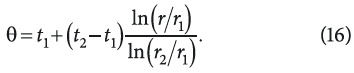
Исходная же зависимая переменная t(r) находится при помощи полуопределенного интегрирования (5) и для случая линейной зависимости λ(t) получим квадратное уравнение вида:

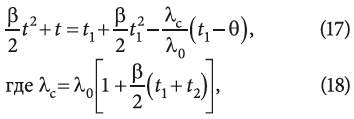
решая которое относительно t (корень из физических соображений берется с положительным знаком радикала) с учетом (16) и (18), получим:

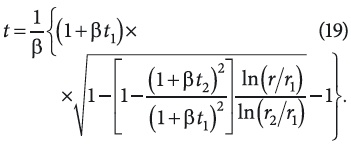
Сравнение случаев постоянного и переменного коэффициентов теплопроводности показывает, что непостоянство коэффициента теплопроводности при β > 0 повышает, а при β < 0 понижает теплообмен. Тогда формула для расчета прироста относительного изменения потока тепла из-за непостоянства коэффициента теплопроводности будет:

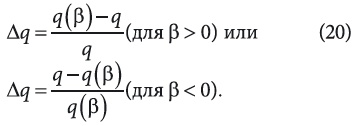
В связи с тем, что термические напряжения сильно (особенно для высокотемпературных процессов) зависят от ∇t, то из (20) следует, что переменная теплопроводность может существенно влиять не только на распределение температур и теплообмен, но также и на величину и распределение термических напряжений, что подтверждается многочисленными практическими примерами из области авиаи машиностроения, а также строительной индустрии и промышленной энергетики.

III. При Γ = 2, линейной зависимости λ(t), Pe = 0 и Po = const общее решение дифференциального уравнения (2) путем следующей промежуточной замены переменной

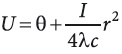
можно свести к решению дифференциального уравнения для ранее рассмотренного случая II (когда Po = 0).

Тогда общее решение уравнения (2) при Po = const с учетом указанной замены запишется в виде:

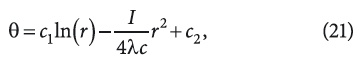
а после определения c₁ и c₂ из краевых условий (3) и (4) решение θ(r) будет:

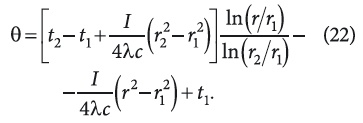
Для более упрощенного изложения алгоритма перехода к исходным переменным поставленной задачи примем t_y = t₂ = 0. Тогда уравнение (22) будет:

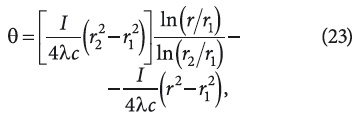
а квадратное уравнение относительно t будет:

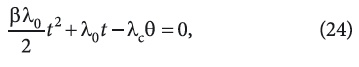
из решения которого следует:

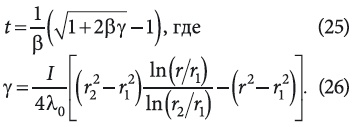
При β = 0 следует, что t = γ, а при β > 0 следует β ≤ 0,5max(γ). Из анализа полученных решений аналогично примеру II выводится оценка температурного профиля в зависимости от λ(t) как при β > 0, так и при β < 0.

IV. При Г = 1, λ = const, Po = const и Pe = 0 решением задачи (6)—(8) будет:

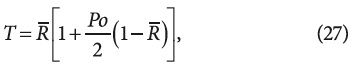
а при совпадении потока тепла с положительным направлением оси r будет:

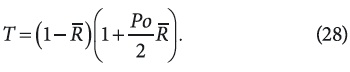
Численные расчеты относительной температуры T(R ) для различных значений Po показали, что в зависимости от значения Po температура стенки может быть заметно больше максимальной температуры поверхности стенки при Po ≥ 3 и меньше минимальной температуры поверхности при Po ≤ -3. Таким образом, чем выше влагосодержание (сток тепла ОК), тем глубже сдвигается фронт конденсации влаги внутрь ОК (зимний период года) и тем шире зона конденсации. Аналогично находятся смещение фронта испарения и сужение зоны конденсации в обратном направлении, то есть к наружной поверхности ОК, когда происходит просушка ограждения (уменьшение влагосодержания и, соответственно, стока тепла в летний период года). Точное расположение фронта и зоны конденсации (испарения) можно найти из условий существования экстремума функции T(R ). Скорость смещения фронта и зоны конденсации (испарения) в том или ином направлении зависит от ∇t, влагосодержания и энергии (формы) связи влаги с материалом ОК. Плотность теплового потока находится из уравнения q = -(dT/dR) и в первоначальных обозначениях при совпадении потока тепла с положительным направлением оси r примет вид:

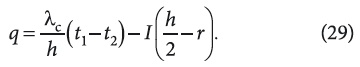
Из (29) следует, что q может быть со знаком «+» при совпадении с положительным направлением оси абсцисс Γ (когда t₁ > t₂), и со знаком «—» при направлении в сторону уменьшения r (когда t₁ < t₂).

Обобщенная постановка задачи (9), (10), (11) позволяет рассмотреть множество других вариаций параметров Γ, λ(t), Pe(T), Po(T) (с учетом направленности потоков и знака ИТ), но алгоритм решения будет аналогичен рассмотренным.

Исходное же уравнение (1) при переменных параметрах переноса [λ(t), Pe(t), Po(t)] и краевых условиях различного рода (возможно смешанных и нелинейных), учитывающих и поверхностные источники (стоки) тепла, в наиболее общем случае решается численными или приближенными методами решения обыкновенных дифференциальных уравнений, а при определенных условиях указанных параметров переноса оно может быть сведено к решению известных дифференциальных уравнений Бесселя, Лежандра или к решению линейного неоднородного дифференциального уравнения n-го порядка (в нашем случае — второго) с переменными коэффициентами следующего вида:

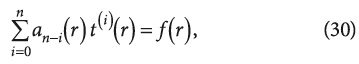
где a_i(r) — переменные коэффициенты неоднородного дифференциального уравнения n-го порядка; (i) — верхний индекс при t означает номер производной, t (0) = t ; α₀ = 1.

Общее решение данного уравнения является следующее выражение:

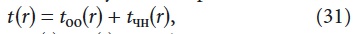
где t_oo(r), t_чн(r) — общее решение однородного уравнения (f(r) = 0) и какоелибо частное решение неоднородного уравнения, соответственно.

Если на некотором интервале известна линейно независимая фундаментальная система решений t_i(i = 1, n) соответствующего однородного уравнения (30), то общее решение неоднородного уравнения может быть найдено методом вариации произвольных постоянных. В этом случае решение уравнения (30) ищем уже в виде [13]:

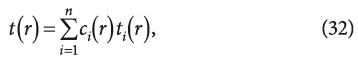
где сi(r) — неизвестные функции находятся из системы n уравнений:

Разрешая систему (33) относительно с_i(r), получим:

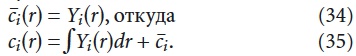
Далее, подставляя полученные значения сi(r) в (32), получим общее решение неоднородного уравнения (30). Например, для уравнения второго порядка система (33) примет вид:

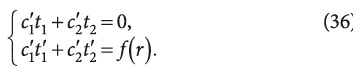
Решая ее относительно с₁ и с₂, определим следущее:

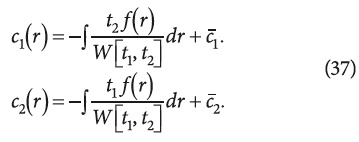
где W(r) — это Вронскиан для данной функций ti(r):

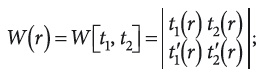
а с_i(i = 1, 2) — произвольные постоянные интегрирования, определяемые из краевых условий задачи.

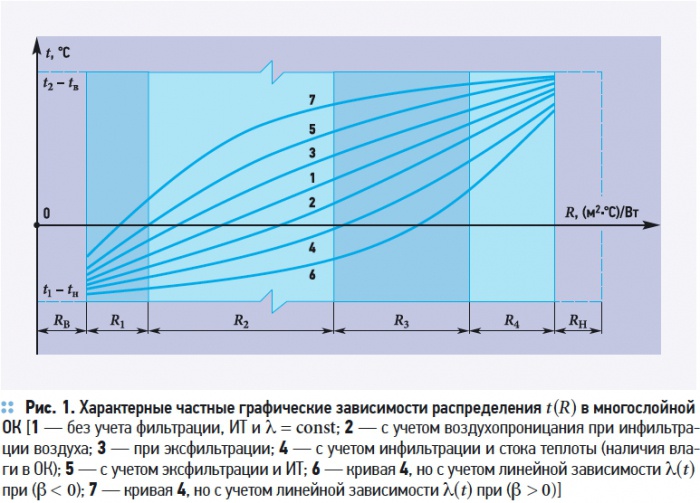
На рис. 1 представлены некоторые характерные профили распределения t(r) в ОК в зависимости от параметров переноса [λ(t), Pe(T), Po(T)] и их знаков.

Заключение

Предлагаемая в критериальном виде обобщенная ММ (9)—(11) процессов нелинейного переноса в многослойной ОК позволяет независимо от масштабов объекта и направления потоков:

— рассчитывать поля температур, тепловые потоки, а также различные коэффициенты переноса (теплоотдачи, теплопередачи, термического сопротивления, порового охлаждения, фильтрационного охлаждения) и др. производные характеристики с учетом ее влагосодержания, различного рода включений или неоднородностей для многообразных классов физических явлений или процессов;

— учитывать в расчетах полей переноса (тепла, влаги, парогазовой смеси) изменение теплофизических характеристик от толщины многослойной ОК или ее термического сопротивления;

— использовать полученные результаты для практических расчетов при проектировании многослойных ОК зданий и сооружений, тепловых инженерных сетей, разработке СНиПов, СП по тепловой защите зданий [14, 15] и т.д.;

— проводить расчеты как тепло-, так и массопереноса различных ОК для канонических систем координат (декартовой — для пластин, стен; цилиндрической — для трубопроводов; сферической — для емкостей): ввиду аналогии законов переноса в приведенных уравнениях символ температуры «t» можно, например, заменить на символ влагосодержания «U», а вместо теплообменных критериев в обобщенной задаче можно использовать массообменные и далее соответственно проинтерпретировать поставленную физическую задачу.