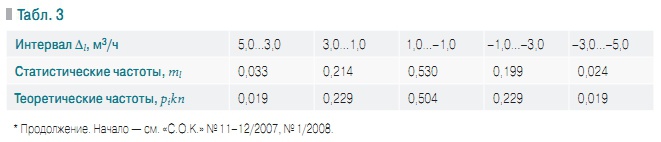
Табл. 3
Среди процессов, явлений, объектов существуют такие, о которых вне зависимости от их величины мы имеем более или менее полное представление. Мы можем представить себе, к примеру, нашу гигантскую по сравнению с нами Землю: ее форму, поверхность, структуру и строение. И вместе с тем, наблюдая ровную поверхность поля или степи, видя ровный горизонт и точно такой же за спиной — поразительно осознавать, что поверхность имеет кривизну и что это одна и та же поверхность.
Случайный поток или процесс представить себе целиком, т.е. всю его генеральную совокупность, невозможно. В конце 60-х гг. прошлого столетия одному из авторов довелось работать на радиоастрономической станции ФИАН в Пущино, где радиотелескопы принимали радиосигналы от далеких нейтронных звезд — пульсаров. Эти сигналы преодолевают огромный путь в сотни и тысячи (наибольший 18 000) световых лет.
Радиосигналы представляют собой случайный процесс с ярко выраженными периодическими импульсами. Очевидно, такой случайный процесс представить в целом практически невозможно, однако по отдельным выборкам ученым удавалось изучить много важного и полезного не только для астрономии, но и для науки вообще. Например, была подтверждена теория относительности Эйнштейна.
И здесь свою роль сыграла проверка статистических гипотез, позволившая по выборке проверить и обосновать то или иное свойство генеральной совокупности — случайного многовекового процесса радиоизлучения звезды. Проверка гипотез заключается в том, что выдвигается одна, так называемая нулевая гипотеза, например для нашего случая, о постоянстве среднеквадратического отклонения σq всего расхода, то есть равенстве его некоторому постоянному значению σq = σq0, а наблюдаемые отклонения вызваны чисто случайными причинами.
Другая, конкурирующая гипотеза может утверждать, что эти отклоненияне случайны, а закономерны. Применяя те или иные критерии проверок гипотез на отдельных выборках, мы не можем подтвердить выдвинутую гипотезу, но можем опровергнуть конкурирующую. В этом суть проверок гипотез. Проверим наши гипотезы, приведенные выше. Начнем с последней, поскольку вид закона распределения, в частности нормальный, лежит в основе проверки остальных гипотез, позволяет упростить применение тех или иных критериев.
Внешний вид гистограммы центрированной составляющей позволяет сделать вывод о принадлежности статистической плотности к нормальному закону, поэтому нулевой гипотезой будет гипотеза о том, что рассматриваемый случайный процесс подчиняется нормальному закону плотности распределения, то есть величина расхождения статистического и теоретического распределения не превосходит допустимое значение.
1. О допустимости величины расхождения теоретической плотности распределения по сравнению с фактически наблюдаемой
В качестве критерия проверки гипотезы применим критерий согласия χ2 Пирсона. Для этого разобьем диапазон изменения случайного потока на l одинаковых интервалов ∆1 = ∆2 = … = ∆l, в нашем случае пять. Подсчитаем для каждого интервала количество значений случайного потока входящих в свой соответствующий интервал и, поделив их на общее число наблюдений, получим статистические частоты ml для всего массива наблюдений — случайных величин потока водопотреблений qi.
Общее количество наблюдение равно произведению количества сечений на число наблюдений в нем: sq = kn = 336. Далее, зная теоретический закон распределения, можно рассчитать вероятность pi попадания каждой наблюдаемой величины в выбранный интервал и определить теоретическую частоту попадания соответствующей величины в свой интервал как произведение вероятности на общее число наблюдений pikn. Получим табл. 3 соответствия статистических и теоретических частот. В нашем случае теоретические частоты рассчитываются исходя из предположения о соответствии наблюдаемой плотности нормальному закону распределения по формуле
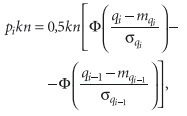
где Φ[(qi – mqi)/ σqi]— интегральная функция распределения или функция Лапласа, Mqi для центрированной случайной составляющей равно нулю. Величину расхождения статистических и теоретических частот определяем по критерию χ2:
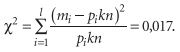
По табл. 3 (символ) — распределения для числа степеней свободы t = l – r – 1 = 1, где r = 3 — число независимых условий наложенных на статистические частоты, к которым относятся следующие:
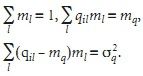
Определяем значение вероятности р, для которой (формула). Для значения (формула) вероятность p = 0,8 является достаточно большой и для рассчитанного значения χ2 = 0,017 величина вероятности будет еще больше. То есть вероятность того, что за счет чисто случайных причин мера расхождения несущественна, велика. Это означает, что величина расхождения наблюдаемой плотности распределений и принятой теоретическойимеет случайный характер и нулевая гипотеза о принадлежности наблюдаемого закона плотности распределения нормальному не может быть отвергнута.
Необходимо отметить, что проведенная выше проверка осуществлена в предположении, что наблюдаемый поток стационарен. Она будет правомерной, если гипотеза об однородности дисперсий будет подтверждена. Для проверки гипотезы об однородности дисперсий в сечениях потока применяют критерий Бартлета, который является самым мощным и более сложным. Однако, если численность выборок, дисперсии которых сравниваются, равны, то можно использовать более простой критерий Кохрана.
2. Об отношении рассчитанных среднеквадратических отклонений к совокупности с одной и той же величиной σ
Критерий Кохрана q представляет отношение максимальной из сравниваемых дисперсий к сумме всех дисперсий. Для нашего случая имеем k = 24 сечения (выборок) с количеством наблюдений n1 = n2 = … = n24 = 14, в которых вычислены дисперсии. Сумма дисперсий равна (уравнение) наибольшее значение дисперсии (уравнение). Величина критерия для совокупности дисперсий в рассматриваемом потоке водопотребления равна:
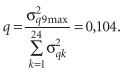
По таблице с надежностью p = 0,95 определяем наименьшее критическое значение критерия, соответствующее большим величинам числа дисперсий (выборок) и числа степеней свободы z = nk – 1, чем в рассматриваемом варианте: qp; k; z = q0,95; 36; 15 = 0,1144. Поскольку вычисленное значение критерия меньше меньшего из теоретических табличных, то можно считать различие дисперсий, а, следовательно, и среднеквадратических отклонений, несущественным.
Таким образом, можно считать, что предположение об отношении рассчитанных среднеквадратических отклонений к разным потокам неверно. Расчет критерия показал, что считать поток нестационарным оснований нет. Наконец, для завершения построения математической модели потока водопотребления необходимо проверить гипотезу о суточной периодичности потока.
3. О равенстве оценок матожидания на границах суточного интервала
На границах суточного интервала имеем две выборки (при условии, что они крайние) с количеством наблюдений n1 = n2 = 14. Кроме того, имеем оценки матожиданий (уравнение) и (уравнение), а также оценки среднеквадратических отклонений (уравнение) и (уравнение). Если нулевая гипотеза справедлива, то статистика вида (при условии n(1 = n2):
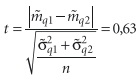
имеет t-распределение Стьюдента. Это означает, что по таблице t-распределения для числа степеней свободы k = n1 + n2 – 2 = 26 и вероятности р = 0,99 можно определить критическое значение tk; p для которого все меньшие вычисленные статистики будут являться признаком опровержения конкурирующей гипотезы, то есть позволят с надежностью р = 0,99 утверждать, что расхождение матожиданий является незначимым. В нашем случае:
t26; 0,99 > t30; 0,99 = 2,756 > t = 0,63,
то можно сделать вывод, что расхождение матожиданий есть результат случайных отклонений. Поскольку причина расхождений матожиданий заключается в случайных отклонениях, то можно сделать вывод: гипотеза о том, что поток водопотребления не имеет суточную периодичность, неверна. В результате теоретических и экспериментальных исследований мы получили достаточно данных, для того чтобы приступить к построению математической модели расхода и обоснованию ее применения для определения потребляемой электронасосом энергии.

























