Вопросам совершенствования методов расчёта процессов тепломассообмена, в частности, для обеспечения адиабатного увлажнения воздуха, посвящён ряд работ Е. В. Стефанова, В. С. Майсоценко, А. Г. Сотникова, О. Я. Кокорина, С. М. Анисимова, М. Г. Тарабанова, А. Г. Аверкина и других [1–8]. Рассмотрены особенности тепломассообмена в различных контактных аппаратах систем кондиционирования воздуха (СКВ). Возможность применения этих процессов в холодный и тёплый периоды года, несомненно, определяет их энергоэффективность [9]. Результаты исследований процессов тепломассообмена в контактных аппаратах получены во многих случаях эмпирическим путём, например, в работах [7, 8]. Это обусловлено сложным характером взаимодействия потоков воздуха и воды, при этом наличие твёрдых поверхностей в насадочных аппаратах ещё более усложняет задачу.
При изучении тепломассобменных процессов в аппаратах контактного типа СКВ важным вопросом является формирование жидкостной плёнки на поверхности орошаемой насадки. В процессе стекания воды по поверхности орошаемой насадки одновременно происходит процесс испарения — таким образом, величина толщины жидкой плёнки становится переменной по высоте поверхности. Толщина плёнки изменяется тем сильнее, чем интенсивнее идёт процесс испарения [10]. В зависимости от высоты изменяются и другие характеристики, такие как расход жидкости, её скорость, линейная массовая плотность орошения, число Рейнольдса. В результате появляется необходимость совместного решения сложной системы уравнений, описывающих процессы испарения жидкой плёнки и её стекания по стенкам насадки.
Современные методы математического моделирования с использованием прикладных программ, обобщённые в работе [11], позволяют получить распределение параметров в различных гидродинамических средах. В работах [10, 12] представлены некоторые результаты численного моделирования процессов тепломассообмена в контактных аппаратах.
Помимо особенностей взаимодействия потоков воды и воздуха, процессы тепломассообмена в насадочных аппаратах существенно зависят от геометрической структуры и теплотехнических характеристик пористых материалов, из которых изготовлена насадка.
Для настоящего исследования при участии авторов модернизирована созданная на кафедре теплогазоснабжения и вентиляции СПбГАСУ установка [10].
В качестве тепломассообменной насадки использована кассета из гигроскопичного материала глубиной 100 мм фирмы Munters. Первые физические исследования и численные эксперименты с использованием прикладной программы StarCCM+ представлены в работе [10]. Однако, учитывая, что подобный численный эксперимент был выполнен впервые и был ограничен по объёму вычислительных процедур, то удалось реализовать численный эксперимент только для исследования одной пластины кассеты.
Реальная кассета состоит из 60 гофрированных листов с длиной волны порядка 17 мм, размещённых поочерёдно под углами к горизонту: 45° вверх и 15° вниз для обеспечения равномерности процесса смачивания и предотвращения отрыва капель.
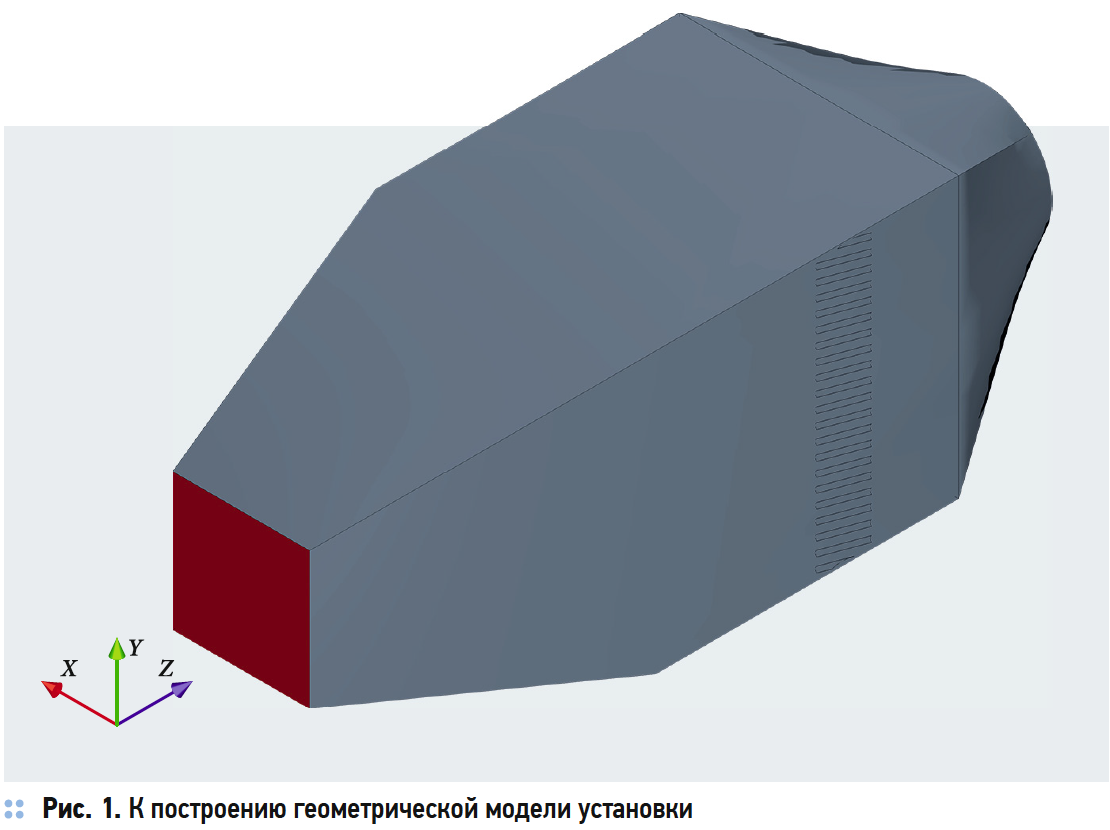
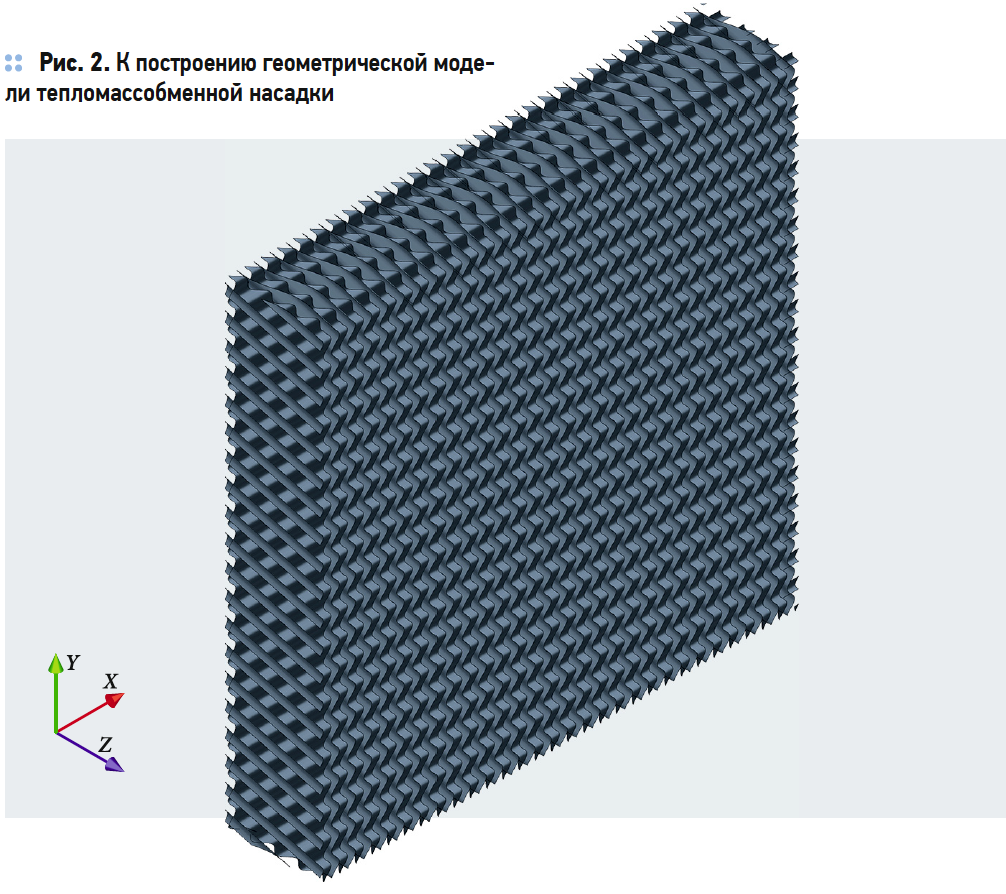
В данной работе для исследования процесса увлажнения воздуха в установке с тепломассообменной насадкой создана геометрическая 3D-модель (рис. 1) установки в программе SolidWorks. Геометрическая модель орошаемой насадки создана отдельным элементом (рис. 2). Габариты насадки соответствуют размерам установки: 510×510×100 мм.
При создании расчётной сетки за базовый принят размер 20 мм. На входе и выходе воздушного потока из установки сетка сгущается до размера 10 мм. Вблизи пластин орошаемой насадки сетка также сгущается, шаг сетки в пять раз меньше базового размера (4 мм). Итоговое количество ячеек расчётной сетки — 2 816 948.
Далее выполнена сборка модели из двух описанных выше деталей в программе SolidWorks. Готовая сборка экспортирована в программу StarCCM+. Последующая работа выполнена в программе StarCCM при помощи встроенных автоматических генераторов: генератора призматического слоя, триммера, генератора поверхностной сетки.
Вблизи пластин и вдоль стенок установки созданы призматические слои с параметрами у пластин: толщина призматических слоёв — 12 мм; число призматических слоёв — четыре; коэффициент растяжения призматических слоёв равен 1,3. Параметры призматических слоёв у стенок установки: толщина призматических слоёв — 24 мм; число призматических слоёв — три; коэффициент растяжения призматических слоёв равен 1,7. Итоговое количество ячеек расчётной сетки — 5 167 824. В сечении канала между пластинами орошаемой насадки в среднем четыре-пять ячеек.
Данное количество является достаточным, но минимальным для формирования достоверной модели движения воздуха в каналах насадки. Создание более подробной расчётной сетки в рамках данной работы не представляется возможным в связи с техническими ограничениями. Указанная выше сетка при расчёте занимает весь максимальный объём оперативной памяти (ОЗУ), обычно доступной на компьютерах для учебного использования.
Расчёт более подробной сетки потребует применения производительного серверного оборудования.
Численное моделирование тепломассообменных процессов в насадке сотового увлажнителя основано на расчёте уравнений Рейнольдса для описания турбулентных потоков, дополненных уравнениями конвективно-диффузионного переноса для осреднённой скалярной субстанции a (температура T, влагосодержание d):
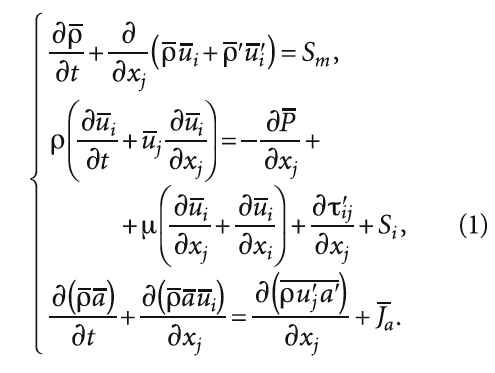
где t — время; ρ — плотность; μ — коэффициент динамической вязкости; uj — компоненты вектора осреднённой скорости по осям координат; τij — турбулентные напряжения (дополнительные напряжения Рейнольдса); ui, uj, T и C — локальные пульсации скорости, температуры и примеси потока; a — осреднённые значения удельной плотности скалярной величины; Sm и Si — интенсивность источников массы и импульса; Ja — интенсивность источников примеси.
В работе совместно решаются две различные задачи:
1. Моделируется турбулентное движение воздуха через орошаемую насадку с адиабатическим охлаждением в ней.
2. Моделируется ламинарное движение (стекание) жидкой плёнки под действием гравитационных сил по орошаемой насадке.
Для численного расчёта исследуемого процесса приняты следующие характеристики: стационарный режим протекания процесса; сила тяжести; излучение вида «поверхность–поверхность»; тепловое излучение серого тела; уравнение энергии среды для температуры; идеальный газ; многокомпонентный газ; k–ε-модель турбулентности; осреднённое по Рейнольдсу уравнение Навье-Стокса.
В качестве граничных условий приняты скорость, температура и относительная влажность воздуха на входе; стационарная температура поверхности стенок установки; температура и относительная влажность воздуха непосредственно на поверхности насадки. При дискретизации расчётной области использована прямоугольная неравномерная сетка, которая сгущается вблизи твёрдых границ согласно закону гиперболического тангенса (алгоритм Винокура). Для учёта особенностей процесса испарения применена Эйлерова многофазность. Для нахождения давления насыщения водяных паров использовано уравнение Антуана.
Известно, что на поверхности гигроскопичной насадки при влажностной обработке воздуха образуется стекающаяся под действием силы тяжести жидкая плёнка. Для нестационарного решателя приняты следующие параметры: единичный шаг по времени — 0,1 с; пять итераций на один шаг времени; расчётное время (в зависимости от расхода воздуха, проходящего через установку, причём при бóльшем расходе воздуха сходимость решения наблюдается быстрее — от трёх до пяти секунд). Время, необходимое для выполнения одной итерации, составило около 70 секунд. Переход от дифференциальных уравнений в частных производных к дискретным осуществлён методом конечных объёмов. При проведении численного эксперимента выполнена оценка сходимости, означающая уменьшение до нуля ошибки численного решения при условии, что размеры контрольных объёмов расчётной области стремятся к нулю. Расчёт считается законченным, если поведение исследуемых параметров становится стационарным.
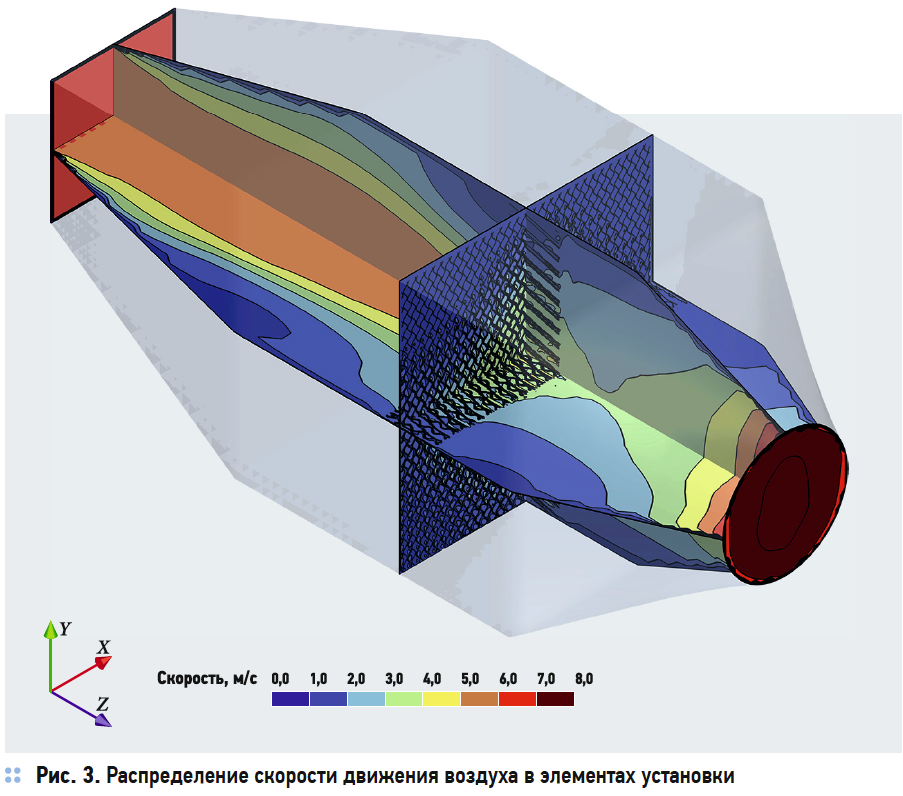
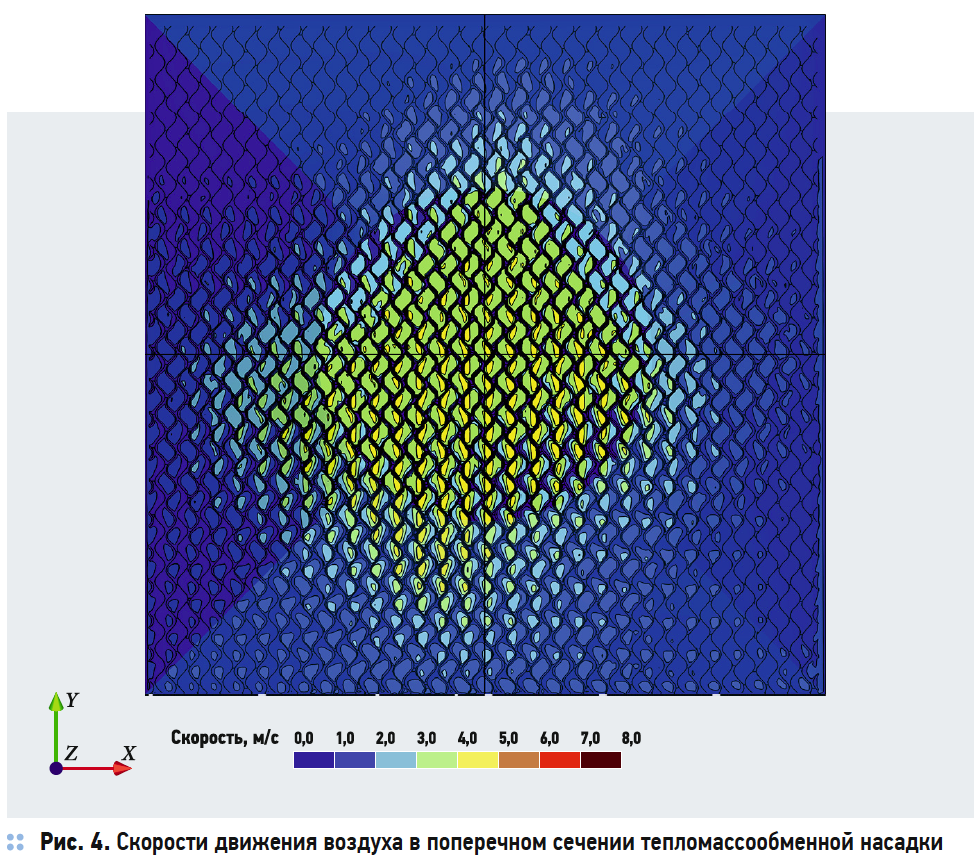
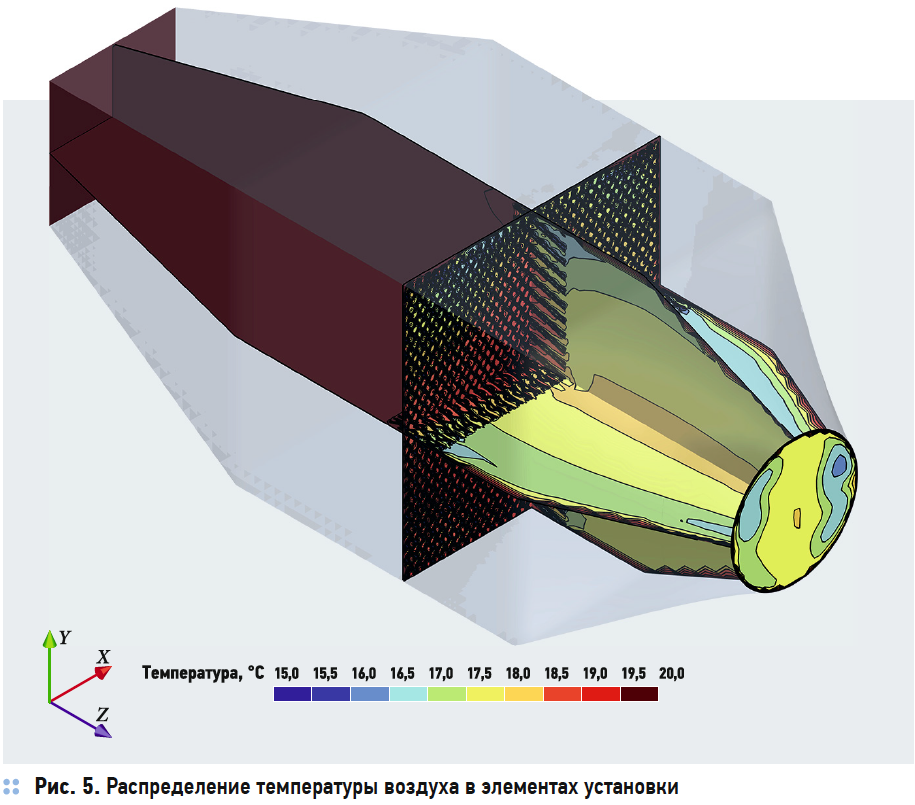
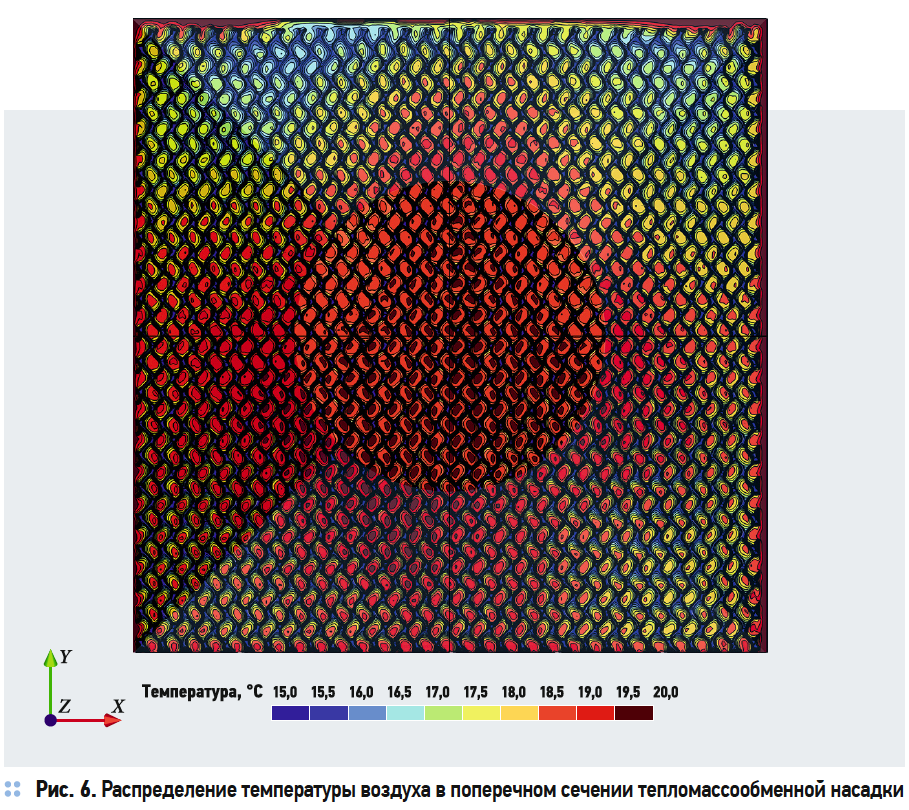
Результаты численного эксперимента представлены на рис. 3–6 в виде полей скоростей и температур в характерных секущих плоскостях.
На основании результатов численного эксперимента определены коэффициенты адиабатической эффективности процесса тепломассообмена в орошаемой насадке. Так, при скорости воздуха в живом сечении насадки 1,4 м/c, начальной температуре воздуха 20 °C и конечной температуре 17,2 °C, соответственно, и при температуре воды 15,1 °C получено значение коэффициента адиабатической эффективности 58 %. Результаты расчёта удовлетворительно соответствуют результатам лабораторного эксперимента.
Заключение
На основании разработанной численной модели на базе k–ε-модели турбулентности впервые получены характеристики тепломассообменных процессов при испарении жидкой плёнки в сотовом увлажнителе реального размера.